
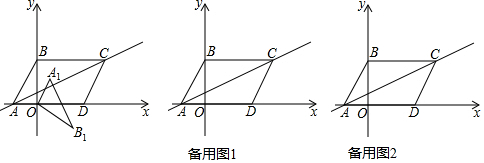
分析 (1)由一次函数解析式可求得A、C两点的坐标,则可求得BC、AD的长,可证得结论;
(2)分三种情况,以直角三角形A1OB1的面积求出斜边上的高,再利用勾股定理即可得出点A1的坐标.
解答 解:(1)当x=16时,n=$\frac{4}{11}×16+\frac{24}{11}$=8,
∴C(16,8),
∵B(0,8),
∴BC=16,BC∥x轴,
当y=0时,0=$\frac{4}{11}x+\frac{24}{11}$,
∴x=-6,
∵D(10,0),
∴BC∥AD,AD=16,∴BC=AD,
∴四边形ABCD为平行四边形;
(2)由(1)知,A(-6,0),B(0,8),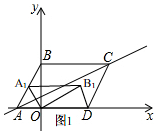
∴OA=6,OB=8,AB=10,
设斜边上的高为h,
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$AB•h,
∴h=$\frac{24}{5}$,
由旋转知,OA1=6,OB1=8,A1B1=10,
当O、A1、D、B1为顶点的四边形是平行四边形,
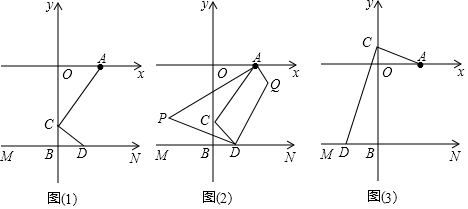
①当OB1为对角线时,如图1,A1B1∥OD,即A1B1⊥y轴于H,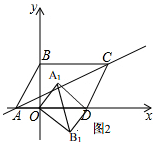
∴OH=h=$\frac{24}{5}$,
在Rt△A1OH中,A1H=$\frac{18}{5}$,
∴1(-$\frac{18}{5}$,$\frac{24}{5}$),
②当OD为对角线时,∠A1OB1=90°,
∴四边形A1OB1D是矩形,
∴∠OA1D=90°,
如图2,过点A1作A1M⊥x轴于M,
同①的方法得出A1M=$\frac{24}{5}$,OM=$\frac{18}{5}$,
∴A1($\frac{18}{5}$,$\frac{24}{5}$)
③当OA1为对角线时,如图3,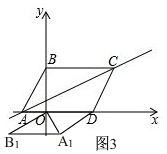 A1B1∥OD,
A1B1∥OD,
∴A1B1⊥y轴于N,
同①的方法,ON=$\frac{24}{5}$,B1N=$\frac{18}{5}$,
∴A1($\frac{18}{5}$,-$\frac{24}{5}$),
即:点A1的坐标为(-$\frac{18}{5}$,$\frac{24}{5}$),($\frac{18}{5}$,$\frac{24}{5}$),($\frac{18}{5}$,-$\frac{24}{5}$).
点评 此题是一次函数综合题,主要考查了旋转的旋转,三角形的面积公式,勾股定理,平行四边形的性质,解(1)的关键是求出点B,C坐标,解(2)的关键是得出A1B1⊥y轴和四边形A1OB1D是矩形,是一道中等难度的中考常考题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
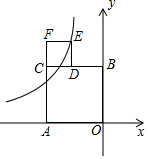 如图,四边形AOBC和四边形CDEF都是正方形,边OA在x轴上,边OB在y轴上,点D在边CB上,反比例函数y=$-\frac{8}{x}$在第二象限的图象经过点E,则正方形AOBC和正方形CDEF的面积之差为( )
如图,四边形AOBC和四边形CDEF都是正方形,边OA在x轴上,边OB在y轴上,点D在边CB上,反比例函数y=$-\frac{8}{x}$在第二象限的图象经过点E,则正方形AOBC和正方形CDEF的面积之差为( )| A. | 12 | B. | 10 | C. | 8 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,数轴上的四个点A,B,C,D对应的数为整数,且AB=BC=CD=1,若|a|+|b|=2,则原点的位置可能是( )
如图,数轴上的四个点A,B,C,D对应的数为整数,且AB=BC=CD=1,若|a|+|b|=2,则原点的位置可能是( )| A. | A或B | B. | B或C | C. | C或D | D. | D或A |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,菱形纸片ABCD中,将纸片沿着BF折叠,使得点A落在点E,当E为CD的中点时,$\frac{BF}{AF}$=( )
如图所示,菱形纸片ABCD中,将纸片沿着BF折叠,使得点A落在点E,当E为CD的中点时,$\frac{BF}{AF}$=( )| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 22.86×104 | B. | 2.286×105 | C. | 2.286×106 | D. | 0.2286×106 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com