
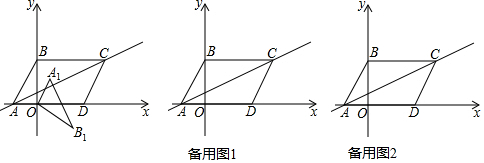
分析 (1)如图1中,作AH⊥AM交CD于H.由△ADH≌△ABM,推出DH=BM,AH=AM,由DN-BM=MN,推出DN-DH=MN推出HN=MN,由△ANH≌△ANM,即可推出∠NAM=∠NAH=45°;
(2)结论:PA+PC=$\sqrt{2}$PD.如图2中,作DQ⊥PC于Q,DG⊥PA于G,PD交AC于O,交AN于T.首先证明△DOC∽△AOP,推出△DOA∽△COP,再证明△PDO≌△PDQ,推出DG=DQ,PG=PQ,易证△ADG≌△CDQ,四边形PQDG是正方形,由此即可解决问题.
(3)如图3中,连接AC.由(2)可知DN-BM=MN,设BM=x则MN=2-x,在Rt△CMN中,由CM2+CN2=MN2,可得(x+1)2+12=(2-x)2,推出x=$\frac{1}{3}$,由(2)可知PC⊥AM,
根据$\frac{1}{2}$•AM•PC=$\frac{1}{2}$•CM•AB,即可求出PC.
解答 (1)证明:如图1中,作AH⊥AM交CD于H.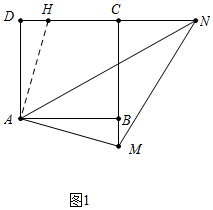
∵∠HAB=∠DAB=90°,
∴∠DAH=∠BAM,
∵∠D=∠ABM=90°,AD=AB,
∴△ADH≌△ABM,
∴DH=BM,AH=AM,
∵DN-BM=MN,
∴DN-DH=MN
∴HN=MN,∵AN=AN,
∴△ANH≌△ANM,
∴∠NAM=∠NAH=45°.
(2)解:结论:PA+PC=$\sqrt{2}$PD.
理由:如图2中,作DQ⊥PC于Q,DG⊥PA于G,PD交AC于O,交AN于T.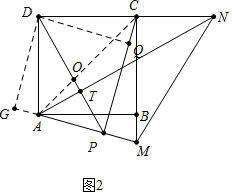
∵PD⊥AN,
∴∠ATP=90°,∵∠PAT=45°,
∴∠APO=∠DCO=45°,∵∠DOC=∠AOP,
∴△DOC∽△AOP,
∴$\frac{DO}{AO}$=$\frac{OC}{OP}$,
∴$\frac{DO}{OC}$=$\frac{AO}{OP}$,∵∠DOA=∠POC,
∴△DOA∽△COP,
∴∠CPD=∠DAO=45°,
∴∠DPA=∠DPC,
∵PD=PD,∠G=∠PQD=90°,
∴△PDO≌△PDQ,
∴DG=DQ,PG=PQ,
易证△ADG≌△CDQ,四边形PQDG是正方形,
∴AQ=CQ,
∴PA+PC=(PG-AG)+(PQ+CQ)=2PG,
∵PD=$\sqrt{2}$PG,
∴PA+PC=$\sqrt{2}$PD.
(3)解:如图3中,连接AC.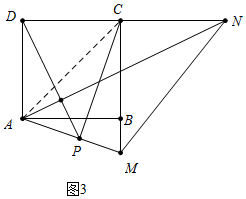
由(2)可知DN-BM=MN,设BM=x则MN=2-x,
在Rt△CMN中,∵CM2+CN2=MN2,
∴(x+1)2+12=(2-x)2,
∴x=$\frac{1}{3}$,
由(2)可知PC⊥AM,
∴$\frac{1}{2}$•AM•PC=$\frac{1}{2}$•CM•AB,
∴PC=$\frac{1×\frac{4}{3}}{\sqrt{{1}^{2}+(\frac{1}{3})^{2}}}$=$\frac{2\sqrt{10}}{5}$.
点评 本题考查正方形的性质和判定、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,题目综合性比较强,属于中考压轴题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:解答题
 为整治城市街道的汽车超速现象,交警大队在某街道旁进行了流动测速.如图,一辆小汽车在某城市街道上直行,某一时刻刚好行驶到离车速检测仪A60m的C处,过了4s后,小汽车到达离车速检测仪A100m的B处,已知该段城市街道的限速为60km/h,请问这辆小汽车是否超速?
为整治城市街道的汽车超速现象,交警大队在某街道旁进行了流动测速.如图,一辆小汽车在某城市街道上直行,某一时刻刚好行驶到离车速检测仪A60m的C处,过了4s后,小汽车到达离车速检测仪A100m的B处,已知该段城市街道的限速为60km/h,请问这辆小汽车是否超速?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
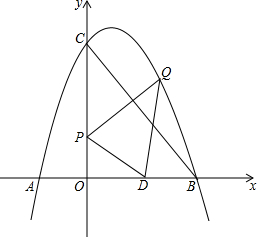 已知抛物线y=$-\frac{1}{3}{x}^{2}+\frac{5}{3}x+12$与x轴交于点A,B(A在B的左侧),与y轴交于点C,连接BC,y轴上的点P(0,m),过点P作BC的垂线交对称轴右侧抛物线于点Q,D为x轴上一动点.
已知抛物线y=$-\frac{1}{3}{x}^{2}+\frac{5}{3}x+12$与x轴交于点A,B(A在B的左侧),与y轴交于点C,连接BC,y轴上的点P(0,m),过点P作BC的垂线交对称轴右侧抛物线于点Q,D为x轴上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30 cm2 | B. | 15 cm2 | C. | 30π cm2 | D. | 15π cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
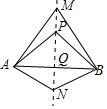 如图,直线MN是四边形AMBN的对称轴,与对角线交与点Q,点P是直线MN上面一点,下列判断错误的是( )
如图,直线MN是四边形AMBN的对称轴,与对角线交与点Q,点P是直线MN上面一点,下列判断错误的是( )| A. | AQ=BQ | B. | AP=BP | C. | ∠MAP=∠MBP | D. | ∠ANM=∠NMB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com