解:(1)把A(-1,0)代入y
2=-x+m得:0=-(-1)+m,
∴m=-1.
把A(-1,0)、B(2,-3)两点代入y
1=ax
2+bx-3得:

,
解得:

,
∴y
1=x
2-2x-3;
(2)∵y
1=x
2-2x-3=(x+1)(x-3),抛物线开口向上,
∴A(-1,0),B(2,-3)
∴当y
2>y
1时,-1<x<2;
(3)∵抛物线y
1=x
2-2x-3=(x-1)
2-4,
∴所求抛物线可由抛物线y=x
2向下平移4个单位,再向右平移1个单位而得到.
分析:(1)因为点A(-1,0)、B(2,-3)都在一次函数和二次函数图象上,一次函数只有一个待定系数m,所以将A(-1,0)、B(2,-3)中任意一点的坐标代入y
2=-x+m即可;二次函数y
1=ax
2+bx-3有两个待定系数a、b,所以需要A(-1,0)、B(2,-3)两点的坐标都代入y
1=ax
2+bx-3,用二元一次方程组解出a、b的值.
(2)直接观察图象中同一个横坐标对应的y
1、y
2的值,直接得到答案;
(3)将所求抛物线解析式配方,写成顶点式,根据顶点坐标确定平移规律.
点评:本题考查了直线与抛物线解析式的求法,抛物线的相关性质的运用.关键是熟练掌握抛物线顶点式与交点式与性质之间的联系.

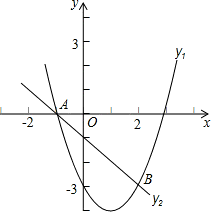 如图,A(-1,0)、B(2,-3)两点在一次函数y2=-x+m与二次函数y1=ax2+bx-3图象上.
如图,A(-1,0)、B(2,-3)两点在一次函数y2=-x+m与二次函数y1=ax2+bx-3图象上. ,
, ,
,

 期末集结号系列答案
期末集结号系列答案 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=