
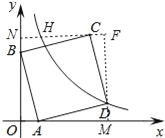
【题目】如图,在平面直角坐标系中,直线y=﹣4x+4与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,将正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线在第一象限的分支上,则a的值是____.
【答案】3
【解析】如图作CN⊥OB于N,DM⊥OA于M,CN与DM交于点F,CN交反比例函数于H,利用三角形全等,求出点C、点H坐标即可解决问题.
解:如图,作CN⊥OB于N,DM⊥OA于M,CN与DM交于点F,CN交反比例函数于H.
∵直线y=﹣4x+4与x轴、y轴分别交于A、B两点,
∴点B(0,4),点A(1,0),
∵四边形ABCD是正方形,
∴AB=AD=DC=BC,∠BAD=90°,
∵∠BAO+∠ABO=90°,∠BAO+∠DAM=90°,
∴∠ABO=∠DAM,
在△ABO和△DAM中,∠BOA=∠AMD=90°,∠ABO=∠DAM,AB=AD,
∴△ABO≌△DAM,
∴AM=BO=4,DM=AO=1,
同理可以得到:CF=BN=AO=1,DF=CN=BO=4,
∴点F(5,5),C(4,1),D(5,1),
设点D在双曲线y=![]() (k≠0)上,则k=5,
(k≠0)上,则k=5,
∴反比例函数为y=![]() ,
,
∴直线CN与反比例函数图象的交点H坐标为(1,5),
∴正方形沿x轴负方向平移a个单位长度后,顶点C恰好落在双曲线y=![]() 上时,a=4﹣1=3,
上时,a=4﹣1=3,
故答案为3.
“点睛”本题考查反比例函数与一次函数的交点、正方形的性质、全等三角形的判定和性质等知识,解题关键是添加辅助线构造全等三角形.


科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,AB∥CD.则添加下列条件,不能使四边形ABCD成为平行四边形的是
A. AD∥BC B. AD=BC C. AB=CD D∠B=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
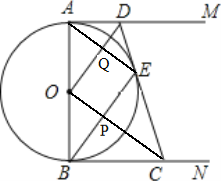
【题目】如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9. 以下结论:
①⊙O的半径为![]() ②OD∥BE ③PB=
②OD∥BE ③PB=![]()
![]() ④tan∠CEP=
④tan∠CEP=![]()
其中正确的结论有( )
A. 1个 B. 2个 C.3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
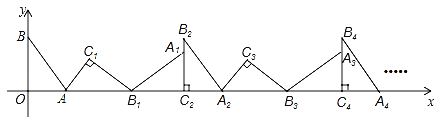
【题目】(2016广东省茂名市第15题)如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则点B2016的坐标为______________.
,0),B(0,2),则点B2016的坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于函数y=-2x+1,下列结论正确的是 ( )
A. 图象必经过(-2,1) B. y随x的增大而增大
C. 图象经过第一、二、三象限 D. 当![]() 时,y<0
时,y<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com