
 |
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源:不详 题型:解答题

 ,sin54°="0.81 " cos54°=0.59,tan54°=1.38,sin70°=0.94,cos70°=0.34,tan70°=2.75)
,sin54°="0.81 " cos54°=0.59,tan54°=1.38,sin70°=0.94,cos70°=0.34,tan70°=2.75)查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 (
( 指缠绕中将部分带子拉成图中所示的平面ABCD时的∠ABC,其中AB为管道侧面母线的一部分).若带子宽度为1,水管直径为4,则
指缠绕中将部分带子拉成图中所示的平面ABCD时的∠ABC,其中AB为管道侧面母线的一部分).若带子宽度为1,水管直径为4,则 的余弦值为 ▲ .
的余弦值为 ▲ . 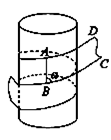
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
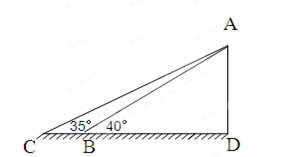
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
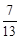 千米,到达对岸AD最少要用 小时。
千米,到达对岸AD最少要用 小时。
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
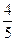 .
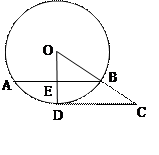
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com