
 如图,一艘轮船在小岛A的北偏东60°方向,距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度是每小时多少海里?
如图,一艘轮船在小岛A的北偏东60°方向,距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度是每小时多少海里? 分析 设该船行驶的速度为x海里/时,由已知可得BC=3x,AQ⊥BC,∠BAQ=60°,∠CAQ=45°,AB=80海里,在直角三角形ABQ中求出AQ、BQ,再在直角三角形AQC中求出CQ,得出BC=40+40$\sqrt{3}$=3x,解方程即可.
解答 解:如图所示:
设该船行驶的速度为x海里/时,3小时后到达小岛的北偏西45°的C处,
由题意得:AB=80海里,BC=3x海里,
在直角三角形ABQ中,∠BAQ=60°,
∴∠B=90°-60°=30°,
∴AQ=$\frac{1}{2}$AB=40,BQ=$\sqrt{3}$AQ=40$\sqrt{3}$,
在直角三角形AQC中,∠CAQ=45°,
∴CQ=AQ=40,
∴BC=40+40$\sqrt{3}$=3x,
解得:x=$\frac{40+40\sqrt{3}}{3}$.
答:该船行驶的速度为$\frac{40+40\sqrt{3}}{3}$海里/时.
点评 本题考查了解直角三角形的应用中的方向角问题、等腰直角三角形的性质、含30°角的直角三角形的性质等知识;通过解直角三角形得出方程是解决问题的关键


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:解答题
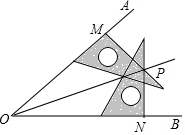 用三角尺可按下面方法画角平分线,在已知的∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB,为什么?
用三角尺可按下面方法画角平分线,在已知的∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB,为什么?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD、AC分别为⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,BO=5,则CD的长为( )
如图,AD、AC分别为⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,BO=5,则CD的长为( )| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,两个村庄A、B在河CD的同侧,A、B两村到河的距离分别为AC=1千米,BD=3千米,CD=3千米.现要在河边CD上建造一水厂,向A、B两村送自来水.铺设水管的工程费用为每千米20000元,请你在CD上选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用W.
如图,两个村庄A、B在河CD的同侧,A、B两村到河的距离分别为AC=1千米,BD=3千米,CD=3千米.现要在河边CD上建造一水厂,向A、B两村送自来水.铺设水管的工程费用为每千米20000元,请你在CD上选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用W.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com