
分析 (1)现在的售价为每件35元,则每件商品降价x元,每件售价为(35-x)元;多买2x件,即每天售量为(50+2x)件,根据每天的销售额=每件售价×每天售量即可得到结论;
(2)每天的销售额=每件售价×每天售量,即y=(35-x)(50+2x),配方后得到y=-2(x-5)2+1800,根据二次函数的性质得到当x=5时,y取得最大值1800.
解答 解:(1)根据题意得:y=(35-x)(50+2x);
(2)∵每天的销售额y=(35-x)(50+2x),(0<x<35)
配方得y=-2(x-5)2+1800,
∵a<0,
∴当x=5时,y取得最大值1800.
答:当每件商品降价5元时,可使每天的销售额最大,最大销售额为l 800元
点评 本题考查了二次函数的应用:根据题意构建二次函数关系式,再利用配方法配成顶点式,然后根据二次函数的性质讨论函数的最大值或最小值.


 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
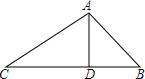 先阅读材料.再解答下面的问题:问题:在△ABC中,AD是边BC上的高,AD=2,DB=2,CD=2$\sqrt{3}$,求∠BAC的度数.
先阅读材料.再解答下面的问题:问题:在△ABC中,AD是边BC上的高,AD=2,DB=2,CD=2$\sqrt{3}$,求∠BAC的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com