
【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.
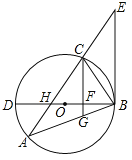
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG=![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)欲证明BE是⊙O的切线,只要证明∠EBD=90°.
(2)由△ABC∽△CBG,得![]() 求出BC,再由△BFC∽△BCD,得
求出BC,再由△BFC∽△BCD,得![]() =BFBD求出BF,CF,CG,GB,再通过计算发现CG=AG,进而可以证明CH=CB,求出AC即可解决问题.
=BFBD求出BF,CF,CG,GB,再通过计算发现CG=AG,进而可以证明CH=CB,求出AC即可解决问题.
试题解析:(1)连接CD,∵BD是直径,∴∠BCD=90°,即∠D+∠CBD=90°,∵∠A=∠D,∠A=∠EBC,∴∠CBD+∠EBC=90°,∴BE⊥BD,∴BE是⊙O切线.
(2)∵CG∥EB,∴∠BCG=∠EBC,∴∠A=∠BCG,∵∠CBG=∠ABC
∴△ABC∽△CBG,∴![]() ,即
,即![]() =BGBA=48,∴BC=
=BGBA=48,∴BC=![]() ,∵CG∥EB,∴CF⊥BD,∴△BFC∽△BCD,∴
,∵CG∥EB,∴CF⊥BD,∴△BFC∽△BCD,∴![]() =BFBD,∵DF=2BF,∴BF=4,在RT△BCF中,CF=
=BFBD,∵DF=2BF,∴BF=4,在RT△BCF中,CF=![]() =
=![]() ,∴CG=CF+FG=
,∴CG=CF+FG=![]() ,在RT△BFG中,BG=
,在RT△BFG中,BG=![]() =
=![]() ,∵BGBA=48,∴BA=
,∵BGBA=48,∴BA=![]() ,即AG=
,即AG=![]() ,∴CG=AG,∴∠A=∠ACG=∠BCG,∠CFH=∠CFB=90°,∴∠CHF=∠CBF,∴CH=CB=
,∴CG=AG,∴∠A=∠ACG=∠BCG,∠CFH=∠CFB=90°,∴∠CHF=∠CBF,∴CH=CB=![]() ,∵△ABC∽△CBG,∴
,∵△ABC∽△CBG,∴![]() ,∴AC=
,∴AC=![]() =
=![]() ,∴AH=AC﹣CH=
,∴AH=AC﹣CH=![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论: ①△AED≌△AEF
②△AED为等腰三角形
③BE+DC>DE
④BE2+DC2=DE2 ,
其中正确的有( )个.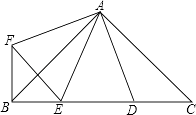
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l上有A、B两点,AB=12cm,点O是线段AB上的一点,OA=2OB.
![]()
(1)OA= cm,OB= cm;
(2)若点C是线段AB上一点,且满足AC=CO+CB,求CO的长;
(3)若动点P、Q分别从A、B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s,设运动时间为ts.当点P与点Q重合时,P、Q两点停止运动.
①当t为何值时,2OP-OQ=4;
②当点P经过点O时,动点M从点O出发,以3cm/s的速度也向右运动.当点M追上点Q后立即返回,以3cm/s的速度向点P运动,遇到点P后再立即返回,以3cm/s的速度向点Q运动,如此往返,直到点P、Q停止时,点M也停止运动.在此过程中,点M行驶的总路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十二五”期间,将新建保障性住房约37000000套,用于解决中低收入和新参加工作的大学生住房的需求,把37000000用科学记数法表示应是( )
A.37×106
B.3.7×106
C.3.7×107
D.0.37×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论: ①甲船的速度是25km/h;
②从A港到C港全程为120km;
③甲船比乙船早1.5小时到达终点;
④图中P点为两者相遇的交点,P点的坐标为( ![]() );
);
⑤如果两船相距小于10km能够相互望见,那么,甲、乙两船可以相互望见时,x的取值范围是 ![]() <x<2.
<x<2.
其中正确的结论有 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com