
【题目】沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论: ①甲船的速度是25km/h;
②从A港到C港全程为120km;
③甲船比乙船早1.5小时到达终点;
④图中P点为两者相遇的交点,P点的坐标为( ![]() );
);
⑤如果两船相距小于10km能够相互望见,那么,甲、乙两船可以相互望见时,x的取值范围是 ![]() <x<2.
<x<2.
其中正确的结论有 . 
【答案】②
【解析】解:甲船的速度为20÷0.5=40km/h,①不成立; 乙船的速度为100÷4=25km/h,
从A港到C港全程为20+100=120km,②成立;
甲船到达C港的时间为120÷40=3(小时),
4﹣3=1小时,③不成立;
设两船相遇的时间为t小时,则有40t﹣25t=20,
解得:t= ![]() ,25×
,25× ![]() =
= ![]() ,
,
即P点坐标为( ![]() ,
, ![]() ),④不成立;
),④不成立;
甲、乙两船第一次相距10km的时间为(20﹣10)÷(40﹣25)= ![]() (小时),
(小时),
甲、乙两船第二次相距10km的时间为(20+10)÷(40﹣25)=2(小时),
甲、乙两船第三次相距10km的时间为(100﹣10)÷25= ![]() (小时),
(小时),
即甲、乙两船可以相互望见时,x的取值范围是 ![]() <x<2和
<x<2和 ![]() <x<4,⑤不成立.
<x<4,⑤不成立.
故答案为:②.
由速度=路程÷时间,可知甲、乙两船的速度,由此可判断①不成立;结合图形中甲的图象可知,A、C两港距离=20+100=120km,由此可判断②成立;由时间=路程÷速度可知甲、乙两船到达C港的时间,由此可判断③不成立;由A港口比B港口离C港口多20km,结合时间=路程÷速度,得出两者相遇的时间,从而判断④不成立;由行驶过程中的路程变化可得出甲、乙两船可以相互望见时,x的取值范围,从而能判断出⑤不成立.由上述即可得出结论.


科目:初中数学 来源: 题型:
【题目】若∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x﹣20)°,则∠α的度数为( )
A.70°
B.86°
C.70°或86°
D.30°或38°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.
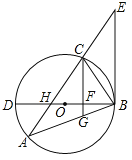
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG=![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=![]() ,
, ![]() ,求BE的长.
,求BE的长.
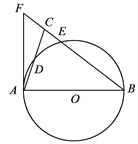
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com