
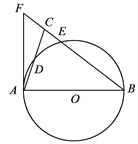
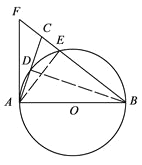
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=![]() ,
, ![]() ,求BE的长.
,求BE的长.
【答案】(1)证明见解析;(2)BE的长为8.
【解析】分析:(1)首先连接BD,由AB为直径,可得∠ADB=90°,又由AF是 O的切线,易证得∠CAF=∠ABD.然后由BA=BC,证得:∠ABC=2∠CAF;
(2)连接AE,利用已知条件分别求出BC,CE的长,由BE=BC-CE计算即可.
本题解析:
(1)证明:连结BD.∵AB是![]() 的直径,∴∠ADB=90°.∴∠DAB+∠DBA=90°.∵AB=AC,∴2∠ABD=∠ABC,AD=
的直径,∴∠ADB=90°.∴∠DAB+∠DBA=90°.∵AB=AC,∴2∠ABD=∠ABC,AD=![]() AC.∵AF为⊙O的切线,∴∠FAB=90°.∴∠FAC+∠CAB=90°.∴∠FAC=∠ABD, ∠ABC=2∠CAF.
AC.∵AF为⊙O的切线,∴∠FAB=90°.∴∠FAC+∠CAB=90°.∴∠FAC=∠ABD, ∠ABC=2∠CAF.
(2)解:连接AE.∴∠AEB=∠AEC=90°.∵sin∠CAF=![]() , ∠ABD=∠CAF=∠CBD=∠CAE∴sin∠ABD=sin∠CAF=
, ∠ABD=∠CAF=∠CBD=∠CAE∴sin∠ABD=sin∠CAF=![]() .∵∠ABD=90°,AC=2
.∵∠ABD=90°,AC=2![]() ,∴AD=
,∴AD=![]() ,AB=
,AB=![]() =10.∵∠AEC=90°,AC=2
=10.∵∠AEC=90°,AC=2![]() ,∴CE=AC·sin∠CAE=2 , ∴BE=BC-CE=10-2=8.
,∴CE=AC·sin∠CAE=2 , ∴BE=BC-CE=10-2=8. 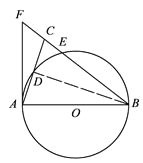


科目:初中数学 来源: 题型:
【题目】月球的直径约为3476000米,将3476000用科学记数法表示应为( )
A.0.3476×102
B.34.76×104
C.3.476×106
D.3.476×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论: ①甲船的速度是25km/h;
②从A港到C港全程为120km;
③甲船比乙船早1.5小时到达终点;
④图中P点为两者相遇的交点,P点的坐标为( ![]() );
);
⑤如果两船相距小于10km能够相互望见,那么,甲、乙两船可以相互望见时,x的取值范围是 ![]() <x<2.
<x<2.
其中正确的结论有 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知A(﹣1,2),B(﹣3,1)C(0,﹣1)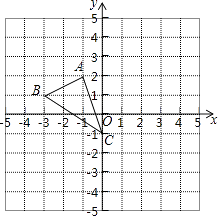
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1
(2)若将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 .
(3)AC的长等于 , △ABC的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
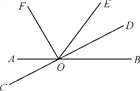
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
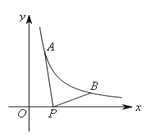
【题目】如图所示,已知A(![]() ,
, ![]() ),B(2,
),B(2, ![]() )为反比例函数y=
)为反比例函数y=![]() 图像上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图像上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
A. (![]() ,0) B. (1,0) C. (
,0) B. (1,0) C. (![]() ,0) D. (
,0) D. (![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有2条,那么该多边形的内角和是_____度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com