
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
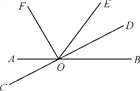
【答案】(1) ∠COE,∠AOD,∠BOC;(2)∠AOD=149°,∠EOF=59°;(3) 射线OD与OF互相垂直,理由见解析.
【解析】试题分析:(1)根据互补的定义确定∠DOE的补角;
(2)先根据角平分线的定义得出∠BOD的度数,再由邻补角定义可得∠AOD=180°-∠BOD;之后根据邻补角定义可得∠AOE=180°-∠BOE,再由角平分线的定义得出∠EOF的度数;
(3)运用平角的定义和角平分线的定义,证明∠DOF是90°,得直线OD、OF的位置关系.
解:(1)∠DOE的补角为:∠COE,∠AOD,∠BOC.
(2)∵OD是∠BOE的平分线,∠BOE=62°,
∴∠BOD=![]() ∠BOE=31°.
∠BOE=31°.
∴∠AOD=180°-∠BOD=149°.
∴∠AOE=180°-∠BOE=118°.
又∵OF是∠AOE的平分线,
∴∠EOF=![]() ∠AOE=59°.
∠AOE=59°.
(3)射线OD与OF互相垂直.理由如下:
∵OF,OD分别是∠AOE,∠BOE的平分线,
∴∠DOF=∠DOE+∠EOF=![]() ∠BOE+
∠BOE+![]() ∠EOA=
∠EOA=![]() (∠BOE+∠EOA)=
(∠BOE+∠EOA)=![]() ×180°=90°.
×180°=90°.
∴OD⊥OF.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校为开展好大课间活动,欲购买单价为20元的排球和单价为80元的篮球共100个.
(1)设购买排球数为x(个),购买两种球的总费用为y(元),请你写出y与x的函数关系式(不要求写出自变量的取值范围);
(2)如果购买两种球的总费用不超过6620元,并且篮球数不少于排球数的3倍,那么有哪几种购买方案?
(3)从节约开支的角度来看,你认为采用哪种方案更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=![]() ,
, ![]() ,求BE的长.
,求BE的长.
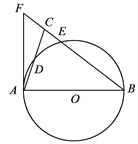
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.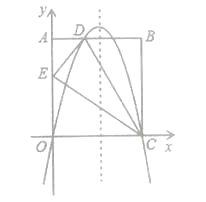
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动,设运动时间为t秒,当t为何值时,以P,Q,C为顶点的三角形与ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分). 目前节能灯在各城市已基本普及,今年某市面向县级及农村地区推广,为响应号召,朝阳灯饰商场用了4200元购进甲型和乙型两种节能灯.这两种型号节能灯的进价、售价如表:
进价(元/只) | 售价(元/只) | |
甲型 | 25 | 30 |
乙型 | 45 | 60 |
特别说明:毛利润=售价﹣进价
(1)朝阳灯饰商场销售甲型节能灯一只毛利润是 元;
(2)朝阳灯饰商场购买甲,乙两种节能灯共100只,其中买了甲型节能灯多少只?
(3)现在朝阳灯饰商场购进甲型节能灯m只,销售完节能灯时所获的毛利润为1080元.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学生共900人,为了解这个年级学生的体能,从中随机抽取部分学生进行1 min的跳绳测试,并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理,下图是这四名同学提供的部分信息:
甲:将全体测试数据分成6组绘成直方图(如图);
乙:跳绳次数不少于105次的同学占96%;
丙:第①、②两组频率之和为0.12,且第②组与第⑥组频数都是12;
丁:第②、③、④组的频数之比为4:17:15。

根据这四名同学提供的材料,下面有四个推断:
①这次跳绳测试共抽取了150人;②该年级跳绳次数的中位数在115~125之间
③第4组的人数为45人 ④如果跳绳次数不少于135次为优秀,根据这次调查结果,估计全年级达到跳绳优秀的人数可以超过250人,其中合理的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com