
【题目】如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.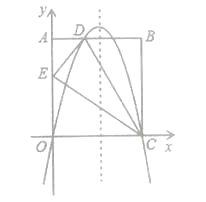
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动,设运动时间为t秒,当t为何值时,以P,Q,C为顶点的三角形与ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x(2)t=
x(2)t=![]() 或
或![]() (3)①M1(4,
(3)①M1(4, ![]() ),N1(4,﹣
),N1(4,﹣![]() );②M2(12,﹣32),N2(4,﹣26);③M3(﹣4,﹣32),N3(4,﹣38).
);②M2(12,﹣32),N2(4,﹣26);③M3(﹣4,﹣32),N3(4,﹣38).
【解析】试题分析:(1)根据折叠图形的轴对称性,△CED、△CBD全等,首先在Rt△CEO中求出OE的长,进而可得到AE的长;在Rt△AED中,AD=AB﹣BD、ED=BD,利用勾股定理可求出AD的长.进一步能确定D点坐标,利用待定系数法即可求出抛物线的解析式.
(2)由于∠DEC=90°,首先能确定的是∠AED=∠OCE,若以P、Q、C为顶点的三角形与△ADE相似,那么∠QPC=90°或∠PQC=90°,然后在这两种情况下,分别利用相似三角形的对应边成比例求出对应的t的值.
(3)由于以M,N,C,E为顶点的四边形,边和对角线都没明确指出,所以要分情况进行讨论:
①EC做平行四边形的对角线,那么EC、MN必互相平分,由于EC的中点正好在抛物线对称轴上,所以M点一定是抛物线的顶点;
②EC做平行四边形的边,那么EC、MN平行且相等,首先设出点N的坐标,然后结合E、C的横、纵坐标差表示出M点坐标,再将点M代入抛物线的解析式中,即可确定M、N的坐标.
试题解析:方法一:
解:(1)∵四边形ABCO为矩形,
∴∠OAB=∠AOC=∠B=90°,AB=CO=8,AO=BC=10.
由题意,△BDC≌△EDC.
∴∠B=∠DEC=90°,EC=BC=10,ED=BD.
由勾股定理易得EO=6.
∴AE=10﹣6=4,
设AD=x,则BD=ED=8﹣x,由勾股定理,得x2+42=(8﹣x)2,
解得,x=3,∴AD=3.
∵抛物线y=ax2+bx+c过点D(3,10),C(8,0),O(0,0)
∴![]() ,
,
解得
∴抛物线的解析式为:y=﹣![]() x2+
x2+![]() x.
x.
(2)∵∠DEA+∠OEC=90°,∠OCE+∠OEC=90°,
∴∠DEA=∠OCE,
由(1)可得AD=3,AE=4,DE=5.
而CQ=t,EP=2t,∴PC=10﹣2t.
当∠PQC=∠DAE=90°,△ADE∽△QPC,
∴![]() ,
,
即![]() ,
,
解得t=![]() .
.
当∠QPC=∠DAE=90°,△ADE∽△PQC,
∴![]() ,
,
即![]() ,
,
解得t=![]() .
.
∴当t=![]() 或
或![]() 时,以P、Q、C为顶点的三角形与△ADE相似.
时,以P、Q、C为顶点的三角形与△ADE相似.
(3)假设存在符合条件的M、N点,分两种情况讨论:
①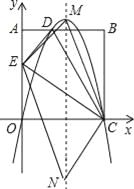
EC为平行四边形的对角线,由于抛物线的对称轴经过EC中点,若四边形MENC是平行四边形,那么M点必为抛物线顶点;
则:M(4, ![]() );而平行四边形的对角线互相平分,那么线段MN必被EC中点(4,3)平分,则N(4,﹣
);而平行四边形的对角线互相平分,那么线段MN必被EC中点(4,3)平分,则N(4,﹣![]() );
);
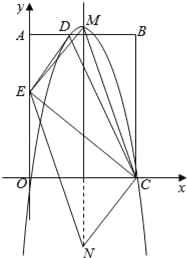
②EC为平行四边形的边,则EC∥MN,EC=,MN设N(4,m),则M(4﹣8,m+6)或M(4+8,m﹣6);
将M(﹣4,m+6)代入抛物线的解析式中,得:m=﹣38,此时 N(4,﹣38)、M(﹣4,﹣32);
将M(12,m﹣6)代入抛物线的解析式中,得:m=﹣26,此时 N(4,﹣26)、M(12,﹣32);
综上,存在符合条件的M、N点,且它们的坐标为:
①M1(﹣4,﹣32),N1(4,﹣38);②M2(12,﹣32),N2(4,﹣26);③M3(4, ![]() ),N3(4,﹣
),N3(4,﹣![]() ).
).



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知A(﹣1,2),B(﹣3,1)C(0,﹣1)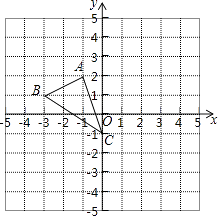
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1
(2)若将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 .
(3)AC的长等于 , △ABC的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
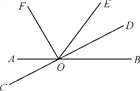
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将某图形的各顶点的横坐标减去2,纵坐标保持不变,可将该图形( )
A.向右平移2个单位
B.向左平移2个单位
C.向上平移2个单位
D.向下平移2个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
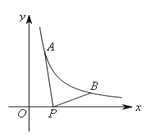
【题目】如图所示,已知A(![]() ,
, ![]() ),B(2,
),B(2, ![]() )为反比例函数y=
)为反比例函数y=![]() 图像上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图像上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
A. (![]() ,0) B. (1,0) C. (
,0) B. (1,0) C. (![]() ,0) D. (
,0) D. (![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b]=b,如:max{4,﹣2}=4,max{3,3}=3,若关于x的函数为y=max{x+3,﹣x+1},则该函数的最小值是( )
A.0
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com