
已知直线y=kx+b(k≠0)过点F(0,1),与抛物线y=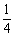 x2相交于B、C两点.
x2相交于B、C两点.
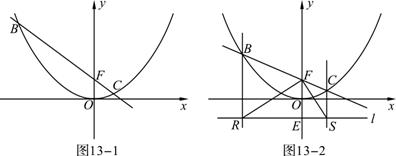
(1)如图13-1,当点C的横坐标为1时,求直线BC的解析式;
(2)在(1)的条件下,点M是直线BC上一动点,过点M作y轴的平行线,与抛物线交于点D,是否存在这样的点M,使得以M、D、O、F为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由;
 (3)如图13-2,设
(3)如图13-2,设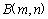 (m<0),过点
(m<0),过点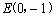 的直线l∥x轴,BR⊥l于R,CS⊥l于S,连接FR、FS.试判断△RFS的形状,并说明理由
的直线l∥x轴,BR⊥l于R,CS⊥l于S,连接FR、FS.试判断△RFS的形状,并说明理由
1)因为点C在抛物线上,所以C(1,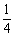 ) ……………………………………………1分
) ……………………………………………1分
又因为直线BC过C、F两点,故得方程组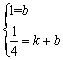 …………………………………………2分
…………………………………………2分
解之,得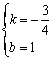 ,所以直线BC的解析式为:
,所以直线BC的解析式为: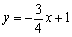 …………………………………3分
…………………………………3分
(2)要使以M、D、O、F为顶点的四边形为平行四边形,则MD=OF
设M(x1, 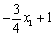 ),则D(x1,
),则D(x1,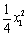 )
)
因为MD∥y轴,所以MD=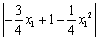 ,由MD=OF,可得
,由MD=OF,可得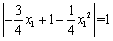 ,
,
①当 时,解得x1=0(舍)或x1=
时,解得x1=0(舍)或x1=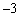 ,所以M(
,所以M(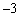 ,
,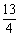 ) ………………5分
) ………………5分
②当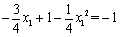 时,解得,
时,解得,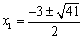 ,
,
所以M(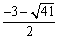 ,
,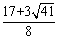 )或M(
)或M(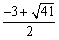 ,
, ), ………………………7分
), ………………………7分
综上所述,存在这样的点M,使以M、D、O、F为顶点的四边形为平行四边形,
M点坐标为(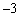 ,
,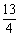 )或(
)或(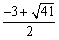 ,
, )或(
)或(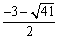 ,
,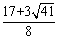 ) ……8分
) ……8分
(3)过点F作FT⊥BR于点T,因为点B在抛物线上,所以m2=4n,在Rt△BTF中,
BF=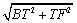 =
=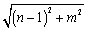 =
=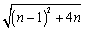 =
=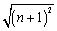 ,因为n>0,所以BF=n+1,
,因为n>0,所以BF=n+1,
又因为BR= n+1,所以BF=BR. 所以∠BRF=∠BFR,………………………………………9分
又因为BR⊥l,EF⊥l,所以BR∥EF,所以∠BRF=∠RFE,
所以∠RFE=∠BFR. …………………………………………………………………………10分
同理可得∠EFS=∠CFS, ……………………………………………………………………11分
所以∠RFS=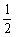 ∠BFC=90°,
∠BFC=90°,
所以△RFS是直角三角形. …………………………………………………………………12分


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.21教育名师原创作品
(1)求篮球和足球的单价;
(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的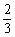 ,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
(3)若购买篮球x个,学校购买这批篮球和足球的总费用为y(元),在(2)的条件下,求哪种方案能使y最小,并求出y的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
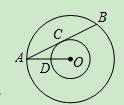
如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB= ,则AB的长是( )
,则AB的长是( )
A. 4 B. 2 C. 8 D. 4
C. 8 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com