
在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
(1)从A、D、E、F四个点中任意取一点,以所取的这一点及点B、C为顶点画三角形,则所画三角形是等腰三角形的概率是 ;
(2)从A、D、E、F四个点中先后任意取两个不同的点,以所取的这两点及点B、C为顶点画四边形,求所画四边形是平行四边形的概率。(用树状图或列表法求解).

(1)P(所画三角形是等腰三角形)=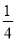 ;(2)P(所画的四边形是平行四边形的概率)=
;(2)P(所画的四边形是平行四边形的概率)=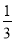 .
.
【解析】
试题分析:(1)根据从A、D、E、F四个点中任意取一点,一共有4种可能,只有选取D点时,所画三角形是等腰三角形,即可得出答案;
(2)利用树状图得出从A、D、E、F四个点中先后任意取两个不同的点,一共有12种可能,进而得出以点A、E、B、C为顶点及以D、F、B、C为顶点所画的四边形是平行四边形,即可求出概率.
试题解析:(1)根据从A、D、E、F四个点中任意取一点,一共有4种可能,只有选取D点时,所画三角形是等腰三角形,
故P(所画三角形是等腰三角形)=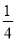 ;
;
(2)用“树状图”或利用表格列出所有可能的结果:

∵以点A、E、B、C为顶点及以D、F、B、C为顶点所画的四边形是平行四边形,
∴P(所画的四边形是平行四边形的概率)=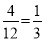 .
.
考点:1.列表法与树状图法2.等腰三角形的判定3.平行四边形的判定.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2013-2014学年江苏省无锡市九年级4月高效课堂调研数学试卷(解析版) 题型:选择题
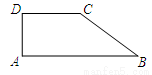
如图,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=8,CD=4,DA=3,则sinB的值是( )
A.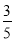 B.
B.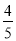 C.
C.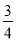 D.
D.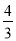
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市崇安区九年级下学期期中统考(一模)数学试卷(解析版) 题型:解答题
演讲答辩由7位评委老师打分,民主测评由50名学生代表一人一票,按“优秀、良好、一般”三选一投票.如图是7位评委对小明“演讲答辩”的评分统计图及50位同学民主测评票数统计图.

(1)求小明演讲答辩所得分数的众数,以及民主测评为“良好”票数的扇形圆心角度数;
(2)求小明的综合得分是多少?
(3)在竞选中,小亮的民主测评得分为82分,如果他的综合得分不小于小明的综合得分,他的演讲答辩得分至少要多少分?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市崇安区九年级下学期期中统考(一模)数学试卷(解析版) 题型:选择题
若5k+20<0,则关于x的一元二次方程x2+4x-k=0的根的情况是( )
A.没有实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.无法判断
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市宜兴外国语学校九年级下学期期中考试数学试卷(解析版) 题型:解答题
矩形纸片ABCD中,AB=5,AD=4.
(1)如图1,四边形MNEF是在矩形纸片ABCD中裁剪出一个正方形.你能否在该矩形中裁剪出一个面积最大的正方形,最大面积是多少?说明理由;
(2)请用矩形纸片ABCD剪拼成一个面积最大的正方形.要求:在图2的矩形ABCD中画出裁剪线,并在网格中画出用裁剪出的纸片拼成的正方形示意图(使正方形的顶点都在网格的格点上).

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市宜兴外国语学校九年级下学期期中考试数学试卷(解析版) 题型:填空题
如图①,在梯形ABCD中,AD∥BC,∠A=60°,动点P从A点出发,以1cm/s的速度沿着A→B→C→D的方向不停移动,直到点P到达点D后才停止.已知△PAD的面积S(单位:cm2)与点P移动的时间(单位:s)的函数如图②所示,则点P从开始移动到停止移动一共用了 秒(结果保留根号).

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市宜兴外国语学校九年级下学期期中考试数学试卷(解析版) 题型:选择题
二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是( )
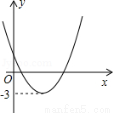
A.k<-3 B.k>-3 C.k<3 D.k>3
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省扬州市邗江区九年级中考一模数学试卷(解析版) 题型:选择题
如图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是

A.①② B.②③ C. ②④ D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com