分析:过点P1作P1E⊥x轴于点E,过点P2作P2F⊥x轴于点F,过点P3作P3G⊥x轴于点G,根据△P1OA1,△P2A1A2,△P3A2A3都是等腰直角三角形,可求出P1,P2,P3的坐标,从而总结出一般规律得出点Pn的坐标.
解答: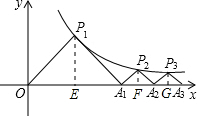
解:过点P
1作P
1E⊥x轴于点E,过点P
2作P
2F⊥x轴于点F,过点P
3作P
3G⊥x轴于点G,
∵△P
1OA
1是等腰直角三角形,
∴P
1E=OE=A
1E=
OA
1,
设点P
1的坐标为(a,a),(a>0),
将点P
1(a,a)代入y=
,可得a=1,
故点P
1的坐标为(1,1),
则OA
1=2a,
设点P
2的坐标为(b+2,b),将点P
2(b+2,b)代入y=
,可得b=
-1,
故点P
2的坐标为(
+1,
-1),
则A
1F=A
2F=
-1,OA
2=OA
1+A
1A
2=2
,
设点P
3的坐标为(c+2
,c),将点P
3(c+2
,c)代入y=
,可得c=
-
,
故点P
3的坐标为(
+
,
-
),
综上可得:P
1的坐标为(1,1),P
2的坐标为(
+1,
-1),P
3的坐标为(
+
,
-
),
总结规律可得:P
n坐标为:(
+
,
-
).
故答案为:(
+
,
-
)、(
+
,
-
).
点评:本题考查了反比例函数的综合,涉及了点的坐标的规律变化,解答本题的关键是根据等腰三角形的性质结合反比例函数解析式求出P1,P2,P3的坐标,从而总结出一般规律,难度较大.

 (2013•泸州)如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数y=
(2013•泸州)如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数y= 解:过点P1作P1E⊥x轴于点E,过点P2作P2F⊥x轴于点F,过点P3作P3G⊥x轴于点G,
解:过点P1作P1E⊥x轴于点E,过点P2作P2F⊥x轴于点F,过点P3作P3G⊥x轴于点G,

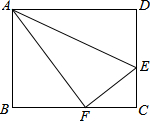 (2013•泸州)如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10
(2013•泸州)如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10 (2013•泸州)如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:
(2013•泸州)如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论: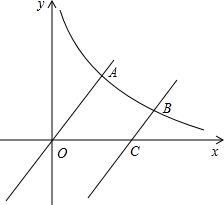 (2013•泸州)如图,已知函数y=
(2013•泸州)如图,已知函数y=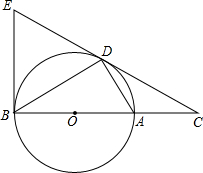 (2013•泸州)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(2013•泸州)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.