
【题目】如图,在矩形ABCD中,AB=10,AD=6,点M为AB上的一动点,将矩形ABCD沿某一直线对折,使点C与点M重合,该直线与AB(或BC)、CD(或DA)分别交于点P、Q
(1)用直尺和圆规在图甲中画出折痕所在直线(不要求写画法,但要求保留作图痕迹)
(2)如果PQ与AB、CD都相交,试判断△MPQ的形状并证明你的结论;
(3)设AM=x,d为点M到直线PQ的距离,y=d2 ,
①求y关于x的函数解析式,并指出x的取值范围;
②当直线PQ恰好通过点D时,求点M到直线PQ的距离.
【答案】
(1)
解:如图1所示:
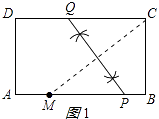
(2)
解:△MPQ是等腰三角形;理由如下:
∵四边形ABCD是矩形,
∴AB∥CD,CD=AB=10,
∴∠QCO=∠PMO,
由折叠的性质得:PQ是CM的垂直平分线,
∴CQ=MQ,OC=OM,
在△OCQ和△OMP中, 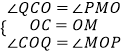 ,
,
∴△OCQ≌△OMP(ASA),
∴CQ=MP,
∴MP=MQ,
即△MPQ是等腰三角形
(3)
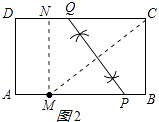
解:①作MN⊥CD于N,如图2所示:
则MN=AD=6,DN=AM=x,CN=10﹣x,
在Rt△MCN中,由勾股定理得:CM2=MN2+CN2,
即(2d)2=62+(10﹣x)2,
整理得:d2= ![]() x2﹣5x+34,
x2﹣5x+34,
即y= ![]() x2﹣5x+34(0≤x≤10);
x2﹣5x+34(0≤x≤10);
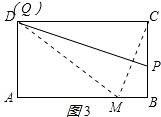
②当直线PQ恰好通过点D时,如图3所示:
则Q与D重合,DM=DC=10,
在Rt△ADM中,AM= ![]() =8,
=8,
∴BM=10﹣8=2,
∴CM= ![]() =
= ![]() =2
=2 ![]() ,
,
∴d= ![]() CM=
CM= ![]() ,
,
即点M到直线PQ的距离为 ![]() .
.
【解析】(1)作线段CM的垂直平分线即可;(2)由矩形的性质得出AB∥CD,CD=AB=10,得出∠QCO=∠PMO,由折叠的性质得出PQ是CM的垂直平分线,由线段垂直平分线的性质得出CQ=MQ,由ASA证明△OCQ≌△OMP,得出CQ=MP,得出MP=MQ即可;(3)①作MN⊥CD于N,如图2所示:则MN=AD=6,DN=AM=x,CN=10﹣x,在Rt△MCN中,由勾股定理得出(2d)2=62+(10﹣x)2 , 即可得出结果;②当直线PQ恰好通过点D时,Q与D重合,DM=DC=10,由勾股定理求出AM,得出BM,再由勾股定理求出CM,即可得出结果.本题是四边形综合题目,考查了矩形的性质、折叠的性质、线段垂直平分线的性质、全等三角形的判定与性质、等腰三角形的判定、勾股定理等知识;本题综合性强,有一定难度,证明三角形全等和运用勾股定理是解决问题的关键.


科目:初中数学 来源: 题型:
【题目】有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣2,0)、B(1,0),直线x=﹣0.5与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC、BC、AD、BD,某同学根据图象写出下列结论:
①a﹣b=0;
②当﹣2<x<1时,y>0;
③四边形ACBD是菱形;
④9a﹣3b+c>0
你认为其中正确的是( )
A.②③④
B.①②④
C.①③④
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=a,BC=b,DE垂直平分AB,则(1)△BEC的周长为_____;(2)若EF=BF,BE⊥AC于E,则∠EFC=______°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.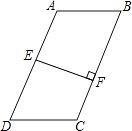
(1)若AB=DC,则四边形ABCD的面积S=;
(2)若AB>DC,则此时四边形ABCD的面积S′ S(用“>”或“=”或“<”填空).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
最喜爱的一种活动统计表
活动形式 | 征文 | 讲故事 | 演讲 | 网上竞答 | 其他 |
人数 | 60 | 30 | 39 | a | b |

(1)在这次抽样调查中,一共调查了多少名学生?扇形统计图中“讲故事”部分的圆心角是多少度?
(2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列文字与例题,并解答:
将一个多项式分组进行因式分解后,可用提公因式法或公式法继续分解的方法称作分组分解法.
例如:以下式子的分解因式的方法就称为分组分解法.
A2+2ab+b2+ac+bc
原式=(a2+2ab+b2)+ac+bc
=(a+b)2+c(a+b)
=(a+b)(a+b+c)
(1)试用“分组分解法”因式分解:![]()
(2)已知四个实数a,b,c,d,满足a≠b,c≠d,并且aa+ac=12k,b2+bc=12k,c2+ac=24k,d2+ad=24k
,同时成立.
①当k=1时,求a+c的值;
②当k≠0时,用含a的代数式分别表示![]() 、
、![]() 、
、![]() (直接写出答案即可).
(直接写出答案即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com