
【题目】如图,抛物线y=x2+x﹣2与x轴交于A,B两点,与y轴交于点C.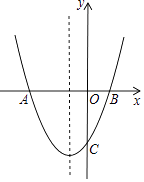
(1)求点A,点B和点C的坐标;
(2)在抛物线的对称轴上有一动点P,求PB+PC的值最小时的点P的坐标;
(3)若点M是直线AC下方抛物线上一动点,求四边形ABCM面积的最大值.
【答案】
(1)
解:由 y=0,得 x2+x﹣2=0 解得 x1=﹣2, x2=1,
∴A(﹣2,0),B(1,0),
由 x=0,得 y=﹣2,
∴C(0,﹣2)
(2)
解:连接AC与对称轴的交点即为点P.
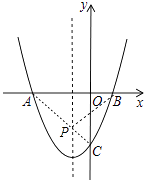
设直线 AC 为 y=kx+b,则﹣2k+b=0,b=﹣2:得 k=﹣1,y=﹣x﹣2.
对称轴为 x=﹣ ![]() ,当 x=﹣
,当 x=﹣ ![]() 时,y=_(﹣
时,y=_(﹣ ![]() )﹣2=﹣
)﹣2=﹣ ![]() ,
,
∴P(﹣ ![]() ,﹣
,﹣ ![]() )
)
(3)
解:过点M作MN丄x轴与点N,
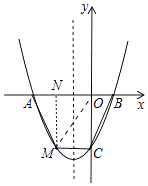
设点M(x,x2+x﹣2),则AN=x+2,0N=﹣x,0B=1,0C=2,MN=﹣(x2+x﹣2)=﹣x2﹣x+2,
S 四边形ABCM=S△AOM+S△OCM+S△BOC= ![]() (x+2)(﹣x2﹣x+2)+
(x+2)(﹣x2﹣x+2)+ ![]() (2﹣x2﹣x+2)(﹣x)+
(2﹣x2﹣x+2)(﹣x)+ ![]() ×1×2
×1×2
=﹣x2﹣2x+3
=﹣(x+1)2+4.
∵﹣1<0,
∴当x=_l时,S四边形ABCM的最大值为4
【解析】(1)利用待定系数法即可解决问题.(2)连接AC与对称轴的交点即为点P.求出直线AC的解析式即可解决问题.(3)过点M作MN丄x轴与点N,设点M(x,x2+x﹣2),则AN=x+2,0N=﹣x,0B=1,0C=2,MN=﹣(x2+x﹣2)=﹣x2﹣x+2,根据S 四边形ABCM=S△AOM+S△OCM+S△BOC构建二次函数,利用二次函数的性质即可解决问题.


科目:初中数学 来源: 题型:
【题目】甲、乙两支清雪队同时开始清理某路段积雪,一段时间后,乙队被调往别处,甲队又用了3小时完成了剩余的清雪任务,已知甲队每小时的清雪量保持不变,乙队每小时清雪50吨,甲、乙两队在此路段的清雪总量y(吨)与清雪时间x(时)之间的函数图象如图所示. 
(1)乙队调离时,甲、乙两队已完成的清雪总量为吨;
(2)求此次任务的清雪总量m;
(3)求乙队调离后y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC= 度.
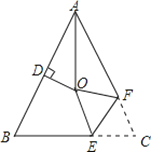
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,D、E、 F分别是△ABC的三边的延长线上一点,且AB=BF,BC=CD,AC=AE,![]() =5cm2,则
=5cm2,则![]() 的值是( )
的值是( )

A. 15 cm2 B. 20 cm2 C. 30 cm2 D. 35 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李大爷一年前买入了A、B两种兔子共46只.目前,他所养的这两种兔子数量相同,且A种兔子的数量比买入时减少了3只,B种兔子的数量比买入时减少a只.
(1)则一年前李大爷买入A种兔子________只,目前A、B两种兔子共________只(用含a的代数式表示);
(2)若一年前买入的A种兔子数量多于B种兔子数量,则目前A、B两种兔子共有多少只?
(3)李大爷目前准备卖出30只兔子,已知卖A种兔子可获利15元/只,卖B种兔子可获利6元/只.如果卖出的A种兔子少于15只,且总共获利不低于280元,那么他有哪几种卖兔方案?哪种方案获利最大?请求出最大获利.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com