
����Ŀ����ͼ����������![]() �ύ��A��
�ύ��A��![]() ��0����B��
��0����B��![]() ��0�����㣬��
��0�����㣬��![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ������
������![]() ,
,![]() �Ƿ���
�Ƿ���![]() ����������
����������
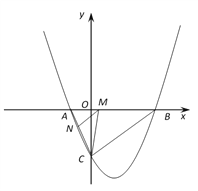
��1���������ߵĽ���ʽ��
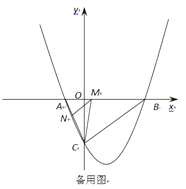
��2����M���߶�AB�ϵ�һ�����㣬����M��MN��BC����AC�ڵ�N������CM������CMN��������ʱ�����M�����ꣻ
��3����D(4��k)�ڣ�1�����������ϣ���EΪ��������һ���㣬��x�����Ƿ���ڵ�F��ʹ��A��D��E��FΪ������ı�����ƽ���ı��Σ�������ڣ�ֱ��д���������������ĵ�F�����꣬�������ڣ���˵�����ɡ�
���𰸡���1��![]() ����2����2��0������3��
����2����2��0������3��![]() .
.
�������������������1������һԪ���η��̽ⷨ�ó�A��B��������꣬�����ý���ʽ������κ�������ʽ��
��2�������ж���MNA�ס�BCA���ó�![]() =
=![]() �������ó���������ֵ��
�������ó���������ֵ��
��3���ֱ���ݵ�AFΪƽ���ı��εı�ʱ��AFƽ���ҵ���DE�뵱AFΪƽ���ı��εĶԽ���ʱ�������ó�����Ҫ��Ĵ𰸣�
���������
��1����![]() ��
��
��![]() ��
�� ![]()
��![]() ��
�� ![]()
�֡������߹���A��B��C��
���������ߵĽ���ʽΪ![]() ��
��
����C��������룬���![]()
�������ߵĽ���ʽΪ![]()
��2�����M������Ϊ��m��0��������N��NH��x���ڵ�H
�ߵ�A������Ϊ��-2��0������B������Ϊ��6��0����
��AB=8��AM=m+2��
��MN��BC��
��. ��MNA�͡�BCA���ƣ�
��![]() ��
��
��![]() ��
��
��![]()
��![]()
![]()
![]()
�൱m=2ʱ�� ![]() �����ֵ4��
�����ֵ4��
��ʱ����M������Ϊ��2��0����
��3���ߵ�D��4��k����������![]() �ϣ�
�ϣ�
�൱x=4ʱ��k=-4��
���D�������ǣ�4��-4����
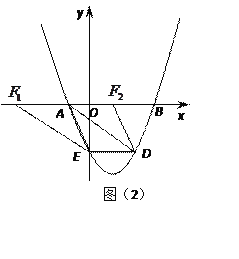
��ͼ��2������AFΪƽ���ı��εı�ʱ��AF![]() DE,AF=DE��
DE,AF=DE��
��D��4��-4������E��0��-4����DE=4��
��F(-6,0)��F(2,0)��
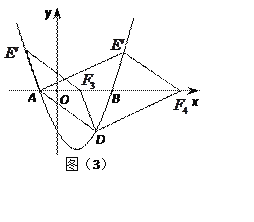
��ͼ��3������AFΪƽ���ı��εĶԽ���ʱ��
��F(n,0)����ƽ���ı��εĶԳ�����Ϊ��![]() ��0����
��0����
��E����������n-6��4����
��E����n-6��4������![]() ����
����
![]()
��� ![]()
��![]() ��
�� ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABO�Ƶ�A˳ʱ����ת����AB1C1��λ�ã���B��O�ֱ����ڵ�B1��C1������B1��x���ϣ��ٽ���AB1C1�Ƶ�B1˳ʱ����ת����A1B1C2��λ�ã���C2��x���ϣ�����A1B1C2�Ƶ�C2˳ʱ����ת����A2B2C2��λ�ã���A2��x���ϣ����ν�����ȥ��������A�� ![]() ��0����B��0��2�������B2016������Ϊ ��
��0����B��0��2�������B2016������Ϊ �� 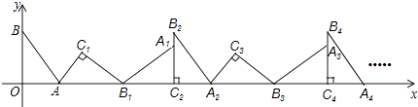
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���O�DZ�AC��һ�����㣬��O��ֱ��MN��BC����MN����ACB��ƽ�����ڵ�E������ACB�����ƽ�����ڵ�F�� 
��1����֤��OE=OF��
��2����CE=8��CF=6����OC�ij���
��3������O�ڱ�AC���˶���ʲôλ��ʱ���ı���AECF�Ǿ��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������ε������ڽǵĺ�Ϊ1800�㣬����������εı���֮��Ϊ2��5��������������εı�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������⣺���ڴ�����ȣ���ͬ���ڽǻ�������ֱ�Ƕ���ȣ�����n��1����n2��1��0������������ĸ����У�������
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A. x3+x3=x6B. x4��x2=x2C. ��m5��5=m10D. x2y3=��xy��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˿�չ���������˶�����ѧ��ÿ���ܶ���һСʱ��ijѧУȥ������Ʒ�̵깺����������������ÿֻ����100Ԫ������ÿֻ����50Ԫ��������Ʒ�̵���ѧУ�ṩ�����Żݷ���������һֻ������һֻ����������������۵�80%�����ѧУҪ����������Ʒ�̵깺������30ֻ������xֻ��x>30����
��1������ѧУ�������ٹ��������踶�� Ԫ�������踶�� Ԫ���ú�x��ʽ�ӱ�ʾ����
����ѧУ�������ڹ��������踶�� Ԫ�������踶�� Ԫ���ú�x��ʽ�ӱ�ʾ����
��2����x=40����ͨ������˵���������١����������ַ��������Ϊ���㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���O�DZ�AC��һ�����㣬��O��ֱ��MN��BC����MN����ACB��ƽ�����ڵ�E������ACB�����ƽ�����ڵ�F�� 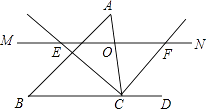
��1����֤��OE=OF��
��2����CE=8��CF=6����OC�ij���
��3������O�ڱ�AC���˶���ʲôλ��ʱ���ı���AECF�Ǿ��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������Ϊ���������(����)
A. �Զ������B. ���x=3����ô|x|=3
C. ֱ�Ƕ����D. �ڴ�����ȣ���ֱ��ƽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com