
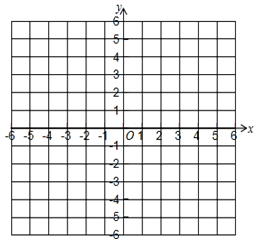
分析 (1)利用配方法即可确定函数的顶点坐标,令y=0求得x就是函数的横坐标,令x=0即可求得与y轴的纵坐标;
(2)根据顶点坐标和与x轴的交点即可作出大体图象,然后根据图象写出x的范围.
解答  解:(1)y=-$\frac{5}{16}$x2+$\frac{5}{8}$x+$\frac{75}{16}$=-$\frac{5}{16}$(x-1)2+5,
解:(1)y=-$\frac{5}{16}$x2+$\frac{5}{8}$x+$\frac{75}{16}$=-$\frac{5}{16}$(x-1)2+5,
则顶点坐标是(1,5);
令y=0,则-$\frac{5}{16}$x2+$\frac{5}{8}$x+$\frac{75}{16}$=0,则解得x=5或-3,
则函数与x轴交于(5,0),(-3,0);
在y=-$\frac{5}{16}$x2+$\frac{5}{8}$x+$\frac{75}{16}$中令x=0,则y=$\frac{75}{16}$,函数与y轴交于(0,$\frac{75}{16}$).
(2)根据图象可得:x≤-3或x≥5时y≤0.
点评 本题考查了配方法求函数的顶点坐标,以及函数与坐标轴的交点的求法,正确应用配方法是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
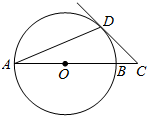 AB是⊙O的直径,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°.
AB是⊙O的直径,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
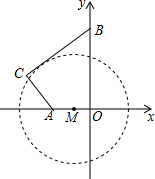 某地质公园为了方便游客,计划修建一条栈道BC连接两条进入观景台OA的栈道AC和OB,其中AC⊥BC,同时为减少对地质地貌的破坏,设立一个圆形保护区⊙M(如图所示),M是OA上一点,⊙M与BC相切,观景台的两端A、O到⊙M上任意一点的距离均不小于80米.经测量,OA=60米,OB=170米,tan∠OBC=$\frac{4}{3}$.
某地质公园为了方便游客,计划修建一条栈道BC连接两条进入观景台OA的栈道AC和OB,其中AC⊥BC,同时为减少对地质地貌的破坏,设立一个圆形保护区⊙M(如图所示),M是OA上一点,⊙M与BC相切,观景台的两端A、O到⊙M上任意一点的距离均不小于80米.经测量,OA=60米,OB=170米,tan∠OBC=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
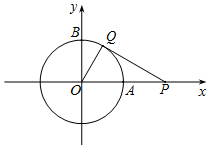 以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.;如图,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时Q走过的路程弧$\widehat{BQ}$的长为 $\frac{π}{6}$;
以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.;如图,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时Q走过的路程弧$\widehat{BQ}$的长为 $\frac{π}{6}$;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com