
【题目】如图,在△ABC中,AB=7,AC=![]() ,∠A=45°,AH⊥HC,垂足为H。
,∠A=45°,AH⊥HC,垂足为H。
(1)求证:△AHC是等腰直角三角形;
(2)求BC的长.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图①,C为线段BE上的一点,分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN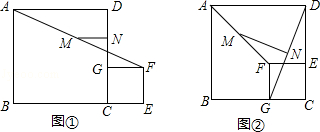
(1)线段MN和GD的数量关系是 , 位置关系是;
(2)将图①中的正方形CEFG绕点C逆时针旋转90°,其他条件不变,如图②,(1)的结论是否成立?说明理由;
(3)已知BC=7,CE=3,将图①中的正方形CEFG绕点C旋转一周,其他条件不变,直接写出MN的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我市某中学在创建“特色校园”的活动中,将奉校的办学理念做成宣传牌(CD),放置在教学楼的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿坡面AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1: ![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1: ![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)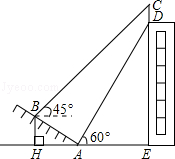
(1)求点B距水平而AE的高度BH;
(2)求宣传牌CD的高度.
(结果精确到0.1米.参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是cm. 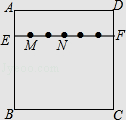
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中, ![]() ,点E是边BC上的动点
,点E是边BC上的动点![]() 不与点
不与点![]() 重合
重合![]() ,以AE为边作
,以AE为边作![]() ,使得
,使得![]() ,射线AF交边CD于点F.
,射线AF交边CD于点F.
![]() 如图1,当点E是边CB的中点时,判断并证明线段
如图1,当点E是边CB的中点时,判断并证明线段![]() 之间的数量关系;
之间的数量关系;
![]() 如图2,当点E不是边BC的中点时,求证:
如图2,当点E不是边BC的中点时,求证: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),我们把P’(y1,x1)叫做点P的友好点,已知点![]() 的友好点为
的友好点为![]() ,点
,点![]() 的友好点为
的友好点为![]() ,点
,点![]() 的友好点为
的友好点为![]() ,…,这样依次得到点.
,…,这样依次得到点.
(1)当点![]() 的坐标为(2,1),则点
的坐标为(2,1),则点![]() 的坐标为___,点
的坐标为___,点![]() 的坐标为___;
的坐标为___;
(2)若![]() 的坐标为(3,2),则设
的坐标为(3,2),则设![]() (x,y),求x+y的值;
(x,y),求x+y的值;
(3)设点A1的坐标为(a,b),若![]() ,
,![]() ,
,![]() ,…
,…![]() ,点
,点![]() 均在y轴左侧,求a、b的取值范围.
均在y轴左侧,求a、b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A=90°,AB=AC , BC=63cm,现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示,已知剪得的纸条中有一张是正方形,则这张正方形纸条是从下往上数第张.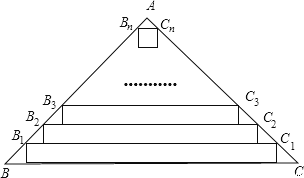
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,求△DCE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com