
如图6,在四边形 中,
中,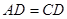 ,
, 平分
平分 ,
,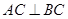 ,
, .
.
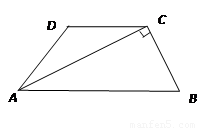
(1)求证:四边形 是等腰梯形;
(6分)
是等腰梯形;
(6分)
(2)取边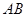 的中点
的中点 ,联结
,联结 .求证:四边形
.求证:四边形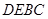 是菱形. (6分)
是菱形. (6分)
见解析
【解析】证明:(1)∵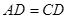 ,∴
,∴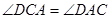
∵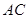 平分
平分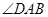 ,
,
∴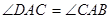
∴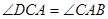 ,
,
∴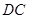 ∥
∥ (2分)
(2分)
在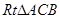 中,
中,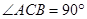 ,
,
∴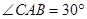 ,
,
∴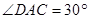 (1分)
(1分)
∴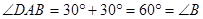 ,
,
∴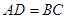 ………………(1分)
………………(1分)
∵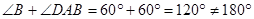
∴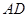 与
与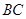 不平行,
(1分)
不平行,
(1分)
∴四边形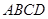 是等腰梯形.
(1分)
是等腰梯形.
(1分)
证明:(2)∵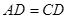 ,
,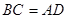 ,
,
∴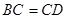 (1分)
(1分)
在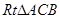 中,
中,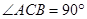 ,
,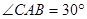
∴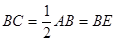 ,
(1分)
,
(1分)
∴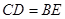 ,
,
∵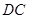 ∥
∥ (2分)
(2分)
∴四边形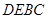 是平行四边形 (1分)
是平行四边形 (1分)
∵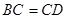
∴四边形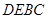 是菱形.
(1分)
是菱形.
(1分)
(1)由等腰三角形的性质、角平分线的性质利用等量代换可以推知内错角∠DCA=∠CAB,利用平行线的判定定理可以证得CD∥AB;然后由直角三角形的性质、角平分线的性质以及等腰三角形 判定定理知AD=BC;最后由等腰梯形的判定定理证得结论;
(2)根据菱形的判定定理(邻边相等的平行四边形是菱形)知,欲证四边形DEBC是菱形,首先证明四边形DEBC是平行四边形,然后结合(1)知邻边CD=BC


科目:初中数学 来源:2012届上海市徐汇初三二模数学试卷(带解析) 题型:解答题
如图6,在四边形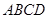 中,
中, ,
,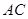 平分
平分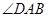 ,
,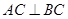 ,
, .
.
(1)求证:四边形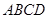 是等腰梯形; (6分)
是等腰梯形; (6分)
(2)取边 的中点
的中点 ,联结
,联结 .求证:四边形
.求证:四边形 是菱形. (6分)
是菱形. (6分)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,在四边形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 的中点,连结
的中点,连结![]() 并延长,分别与
并延长,分别与![]() 的延长线交于点
的延长线交于点![]() ,则
,则![]() (不需证明).
(不需证明).
(温馨提示:在图1中,连结![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() ,根据三角形中位线定理,证明
,根据三角形中位线定理,证明![]() ,从而
,从而![]() ,再利用平行线性质,可证得
,再利用平行线性质,可证得![]() .)
.)
问题一:如图2,在四边形![]() 中,
中,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点,连结
的中点,连结![]() ,分别交
,分别交![]() 于点
于点![]() ,判断
,判断![]() 的形状,请直接写出结论.
的形状,请直接写出结论.
问题二:如图3,在![]() 中,
中,![]() ,
,![]() 点在
点在![]() 上,
上,![]() ,
,![]() 分别是
分别是![]() 的中点,连结
的中点,连结![]() 并延长,与
并延长,与![]() 的延长线交于点
的延长线交于点![]() ,若
,若![]() ,连结
,连结![]() ,判断
,判断![]() 的形状并证明.
的形状并证明.
 |
查看答案和解析>>
科目:初中数学 来源:模拟题 题型:解答题
 中,
中, ,
, ,∠A=60°,∠B﹦∠D﹦90°, 求四边形
,∠A=60°,∠B﹦∠D﹦90°, 求四边形 的面积;
的面积; 中,AB∥CD,CE是∠
中,AB∥CD,CE是∠ 的平分线,且CE⊥AD,
的平分线,且CE⊥AD, ,CE把梯形
,CE把梯形 分成面积为
分成面积为 和S2的两部分,若
和S2的两部分,若 ﹦1,求
﹦1,求 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,在四边形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 的中点,连结
的中点,连结![]() 并延长,分别与
并延长,分别与![]() 的延长线交于点
的延长线交于点![]() ,则
,则![]() (不需证明).
(不需证明).
(温馨提示:在图1中,连结![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() ,根据三角形中位线定理,证明
,根据三角形中位线定理,证明![]() ,从而
,从而![]() ,再利用平行线性质,可证得
,再利用平行线性质,可证得![]() .)
.)
问题一:如图2,在四边形![]() 中,
中,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点,连结
的中点,连结![]() ,分别交
,分别交![]() 于点
于点![]() ,判断
,判断![]() 的形状,请直接写出结论.
的形状,请直接写出结论.
问题二:如图3,在![]() 中,
中,![]() ,
,![]() 点在
点在![]() 上,
上,![]() ,
,![]() 分别是
分别是![]() 的中点,连结
的中点,连结![]() 并延长,与
并延长,与![]() 的延长线交于点
的延长线交于点![]() ,若
,若![]() ,连结
,连结![]() ,判断
,判断![]() 的形状并证明.
的形状并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com