
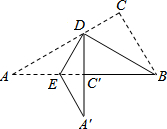
 如图,在Rt△ABC中,∠ACB=90°,将△ABC沿BD折叠,点C恰巧落在边AB上的C′处,折痕为BD,再将其沿DE折叠,使点A落在DC′的延长线上的A′处.若△BED与△ABC相似,则相似比$\frac{BD}{AC}$=$\frac{2}{3}$.
如图,在Rt△ABC中,∠ACB=90°,将△ABC沿BD折叠,点C恰巧落在边AB上的C′处,折痕为BD,再将其沿DE折叠,使点A落在DC′的延长线上的A′处.若△BED与△ABC相似,则相似比$\frac{BD}{AC}$=$\frac{2}{3}$. 分析 根据△BED与△ABC相似和△ABC沿BD折叠,点C恰巧落在边AB上的C′处,求出∠A=∠DBA=∠DBC=30°,利用三角函数求出BD、AC的长,得到答案.
解答 解:△BED与△ABC相似,
∴∠DBA=∠A,又∠DBA=∠DBC,
∴∠A=∠DBA=∠DBC=30°,
设BC为x,
则AC=$\sqrt{3}$x,BD=$\frac{2\sqrt{3}}{3}$x,
$\frac{BD}{AC}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题考查的是相似三角形的性质和翻折变换的知识,掌握相似三角形的对应角相等和锐角三角函数的应用是解题的关键.


科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系xOy中,一次函数y=-x+b的图象与反比例函数y=-$\frac{1}{x}$(x<0)交于点A,与x轴交于点B,则OA2-OB2的值为( )
如图,在平面直角坐标系xOy中,一次函数y=-x+b的图象与反比例函数y=-$\frac{1}{x}$(x<0)交于点A,与x轴交于点B,则OA2-OB2的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
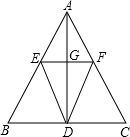 如图所示,在等腰△ABC中,AB=AC,AD是BC边上的高,点E,F分别是边AB,AC上的点,且EF∥BC,AD与EF交于点G.
如图所示,在等腰△ABC中,AB=AC,AD是BC边上的高,点E,F分别是边AB,AC上的点,且EF∥BC,AD与EF交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:| 类别 | 人数 | 占总人数比例 |
| 重视 | a | b |
| 一般 | 57 | 0.285 |
| 不重视 | c | 0.36 |
| 说不清楚 | 9 | 0.045 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com