
【题目】张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米.假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
(1)求张师傅加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式;
(2)求出a的值;
(3)求张师傅途中加油多少升?
【答案】
(1)解:设加油前函数解析式为y=kt+b(k≠0),
把(0,28)和(1,20)代入,
得 ![]() ,
,
解得: ![]() ,
,
故张师傅加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式为:y=﹣8t+28
(2)解:当y=0时,﹣8t+28=0,
解得:t= ![]() ,
,
故a= ![]() ﹣
﹣ ![]() =3
=3
(3)解:设途中加油x升,则28+x﹣34=8× ![]() ,
,
解得:x=46,
答:张师傅途中加油46升
【解析】(1)由图中所给条件和待定系数法易得加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式。
(2)设若没有加油,则用完油时,Y=0,求得此时t=![]() ,又知加油时,车载电脑显示还能行驶50千米,则距实际时间还差
,又知加油时,车载电脑显示还能行驶50千米,则距实际时间还差![]() 小时,最后易得a=3.
小时,最后易得a=3.
(3)由5小时后还有34升油易得方程28+x﹣34=8×5,求得加了46升油。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
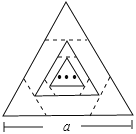
【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,则不难证明S1=S2+S3 .
(1) 如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3之间有什么关系?(不必证明)
(2) 如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系并加以证明;
(3) 若分别以直角三角形ABC三边为边向外作三个正多边形,其面积分别用S1、S2、S3表示,请你猜想S1、S2、S3之间的关系?.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).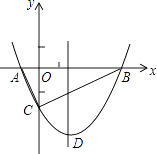
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com