
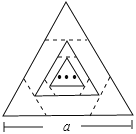
【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
连接AD、DB、DF,求出∠AFD=∠ABD=90°,根据HL证两三角形全等得出∠FAD=60°,求出AD∥EF∥GI,过F作FZ⊥GI,过E作EN⊥GI于N,得出平行四边形FZNE得出EF=ZN=![]() a,求出GI的长,求出第一个正六边形的边长是
a,求出GI的长,求出第一个正六边形的边长是![]() a,是等边三角形QKM的边长的
a,是等边三角形QKM的边长的![]() ;同理第二个正六边形的边长是等边三角形GHI的边长的
;同理第二个正六边形的边长是等边三角形GHI的边长的![]() ;求出第五个等边三角形的边长,乘以
;求出第五个等边三角形的边长,乘以![]() 即可得出第六个正六边形的边长.
即可得出第六个正六边形的边长.
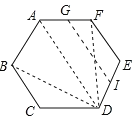
连接AD、DF、DB.
∵六边形ABCDEF是正六边形,
∴∠ABC=∠BAF=∠AFE,AB=AF,∠E=∠C=120°,EF=DE=BC=CD,
∴∠EFD=∠EDF=∠CBD=∠BDC=30°,
∵∠AFE=∠ABC=120°,
∴∠AFD=∠ABD=90°,
在Rt△ABD和RtAFD中
![]()
∴Rt△ABD≌Rt△AFD(HL),
∴∠BAD=∠FAD=![]() ×120°=60°,
×120°=60°,
∴∠FAD+∠AFE=60°+120°=180°,
∴AD∥EF,
∵G、I分别为AF、DE中点,
∴GI∥EF∥AD,
∴∠FGI=∠FAD=60°,
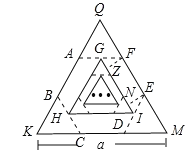
∵六边形ABCDEF是正六边形,△QKM是等边三角形,
∴∠EDM=60°=∠M,
∴ED=EM,
同理AF=QF,
即AF=QF=EF=EM,
∵等边三角形QKM的边长是a,
∴第一个正六边形ABCDEF的边长是![]() a,即等边三角形QKM的边长的
a,即等边三角形QKM的边长的![]() ,
,
过F作FZ⊥GI于Z,过E作EN⊥GI于N,
则FZ∥EN,
∵EF∥GI,
∴四边形FZNE是平行四边形,
∴EF=ZN=![]() a,
a,
∵GF=![]() AF=
AF=![]() ×
×![]() a=
a=![]() a,∠FGI=60°(已证),
a,∠FGI=60°(已证),
∴∠GFZ=30°,
∴GZ=![]() GF=
GF=![]() a,
a,
同理IN=![]() a,
a,
∴GI=![]() a+
a+![]() a+
a+![]() a=
a=![]() a,即第二个等边三角形的边长是
a,即第二个等边三角形的边长是![]() a,与上面求出的第一个正六边形的边长的方法类似,可求出第二个正六边形的边长是
a,与上面求出的第一个正六边形的边长的方法类似,可求出第二个正六边形的边长是![]() ×
×![]() a;
a;
同理第第三个等边三角形的边长是![]() ×
×![]() a,与上面求出的第一个正六边形的边长的方法类似,可求出第三个正六边形的边长是
a,与上面求出的第一个正六边形的边长的方法类似,可求出第三个正六边形的边长是![]() ×
×![]() ×
×![]() a;
a;
同理第四个等边三角形的边长是![]() ×
×![]() ×
×![]() a,第四个正六边形的边长是
a,第四个正六边形的边长是![]() ×
×![]() ×
×![]() ×
×![]() a;
a;
第五个等边三角形的边长是![]() ×
×![]() ×
×![]() ×
×![]() a,第五个正六边形的边长是
a,第五个正六边形的边长是![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() a;
a;
第六个等边三角形的边长是![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() a,第六个正六边形的边长是
a,第六个正六边形的边长是![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() a,
a,
即第六个正六边形的边长是![]() ×
×![]() a,
a,
故选A.


科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,进价是20元,根据市场调查:在一段时间内,销售单价是30元时,销售量是500件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>30),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) | |
销售玩具获得利润w(元) |
(2)在(1)问条件下,若商场获得了8000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于35元,且商场要完成不少于350件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1正方形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点,3AE=EB,有一只蚂蚁从E点出发,经过F、G、H,最后回点E点,则蚂蚁所走的最小路程是( )

A.2B.4C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
我们知道:一条线段有两个端点,线段![]() 和线段
和线段![]() 表示同一条线段. 若在直线
表示同一条线段. 若在直线![]() 上取了三个不同的点,则以它们为端点的线段共有 条;若取了四个不同的点,则共有线段 条;…;依此类推,取了
上取了三个不同的点,则以它们为端点的线段共有 条;若取了四个不同的点,则共有线段 条;…;依此类推,取了![]() 个不同的点,共有线段条.(用含
个不同的点,共有线段条.(用含![]() 的代数式表示)
的代数式表示)
类比探究:
以一个锐角的顶点为端点向这个角的内部引射线.
(1)若引出两条射线,则所得图形中共有 个锐角;
(2)若引出![]() 条射线,则所得图形中共有 个锐角.(用含
条射线,则所得图形中共有 个锐角.(用含![]() 的代数式表示)
的代数式表示)
拓展应用:
一条铁路上共有8个火车站,若一列火车往返过程中必须停靠每个车站,则铁路局需为这条线路准备多少种车票?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB= ![]() πcm2;②
πcm2;② ![]() ;③∠ACB=20°;④∠ADB=140°.错误的有( )
;③∠ACB=20°;④∠ADB=140°.错误的有( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D,E分别是AC,AB上的点,BD与CE交于点O.给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.上述三个条件中,哪两个条件可判定△ABC是等腰三角形(用序号写出一种情形):_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米.假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
(1)求张师傅加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式;
(2)求出a的值;
(3)求张师傅途中加油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队修建一条长1200 m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com