
【题目】在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为________cm2.
科目:初中数学 来源: 题型:
【题目】已知地球距离月球表面约为383 900千米,那么这个距离用科学记数法表示为 ( )
A. 3.839×104 千米 B. 3.839×105千米
C. 3.839×106千米 D. 38.39×104千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于直角三角形的说法中错误的是( )
A. 直角三角形的两个锐角互余
B. 直角三角形斜边的中点到三个顶点的距离相等
C. 直角三角形斜边上的高等于斜边的一半
D. 直角三角形中有两条边的平方和等于第三条边的平方
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图。 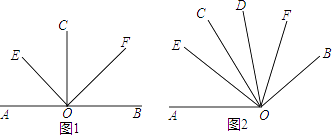
(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;
(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;
(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC= . (用含α与β的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如图:
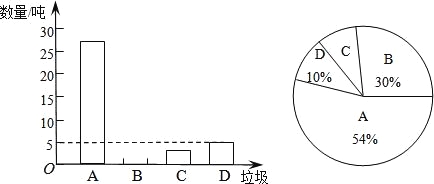
(注:A为可回收物,B为厨余垃圾,C为有害垃圾,D为其他垃圾)
根据图表解答下列问题:
(1)在抽样数据中,产生的有害垃圾共多少吨?
(2)请将条形统计图补充完整;
(3)调查发现,在可回收物中塑料类垃圾占![]() ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京故宫有着近六百年的历史,是最受中外游客喜爱的景点之一,其年接待量在2019年首次突破19000000人次大关.将19000000用科学记数法可表示为( )
A.0.19×108B.0.19×107C.1.9×107D.19×106
查看答案和解析>>
科目:初中数学 来源: 题型:
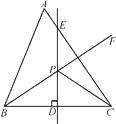
【题目】(12分)如图,在△ABC中,∠A=60°,点D是BC边的中点,DE⊥BC,∠ABC的平分线BF交DE于△ABC内一点P,连接PC.
(1)若∠ACP=24°,求∠ABP的度数;
(2)若∠ACP=m°,∠ABP=n°,请直接写出m,n满足的关系式:_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一个锐角的余角比这个角的补角小90°;
B. 如果一个角有补角,那么这个角必是钝角;
C. 若∠1+∠2+∠3=180°,则∠1、∠2、∠3互为补角;
D. 如果∠α和∠β互为余角,∠β与∠θ互为余角,那么∠α与∠θ互为余角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com