
我们知道,一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到(如图).
类似地,函数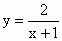 的图象与
的图象与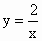 的图象有什么关系呢?
的图象有什么关系呢?
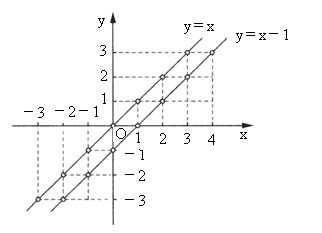
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
 (2013•镇江)通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数y=
(2013•镇江)通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数y=| k |
| x+2 |
| k |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| |A×m+B×n+C| | ||
|

| 5 |
| 12 |
| 1 |
| 6 |
| 5 |
| 12 |
| 1 |
| 6 |
| |5×1+(-12)×2+(-2)| | ||
|
| 21 |
| 13 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数
通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数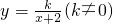 的图象是由反比例函数
的图象是由反比例函数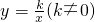 的图象向左平移2个单位长度得到.灵活运用这一知识解决问题.
的图象向左平移2个单位长度得到.灵活运用这一知识解决问题. 的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B.
的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B. 的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C′和l′,已知图象C′经过点M(2,4).
的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C′和l′,已知图象C′经过点M(2,4).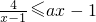 的解集.
的解集.查看答案和解析>>
科目:初中数学 来源:2013届江苏省无锡市前洲中学九年级下学期期中考试数学试卷(带解析) 题型:解答题
阅读下列材料:
我们知道,一次函数y=kx+b的图象是一条直线,而y=kx+b经过恒等变形可化为直线的另一种表达形式:Ax+Bx+C=0(A、B、C是常数,且A、B不同时为0).如图1,点P(m,n)到直线l:Ax+Bx+C=0的距离(d)计算公式是:d= .
.
例:求点P(1,2)到直线y= x-
x- 的距离d时,先将y=
的距离d时,先将y= x-
x- 化为5x-12y-2=0,再由上述距离公式求得d=
化为5x-12y-2=0,再由上述距离公式求得d= =
= .
.
解答下列问题:
如图2,已知直线y=- x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
(1)求点M到直线AB的距离.
(2)抛物线上是否存在点P,使得△PAB的面积最小?若存在,求出点P的坐标及△PAB面积的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(江苏镇江卷)数学(解析版) 题型:解答题
通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x﹣1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数 的图象是由反比例函数
的图象是由反比例函数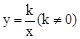 的图象向左平移2个单位长度得到.灵活运用这一知识解决问题.
的图象向左平移2个单位长度得到.灵活运用这一知识解决问题.
如图,已知反比例函数 的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B.
的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B.
(1)写出点B的坐标,并求a的值;
(2)将函数 的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C′和l′,已知图象C′经过点M(2,4).
的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C′和l′,已知图象C′经过点M(2,4).
①求n的值;
②分别写出平移后的两个图象C′和l′对应的函数关系式;
③直接写出不等式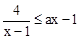 的解集.
的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com