
����Ŀ����ͼ���Ե�P��-1,0��ΪԲ�ĵ�Բ����x����B��C���㣨B��C����ࣩ����y����A��D���㣨A��D���·�����AD=![]() ������ABC�Ƶ�P��ת180�����õ���MCB��
������ABC�Ƶ�P��ת180�����õ���MCB��

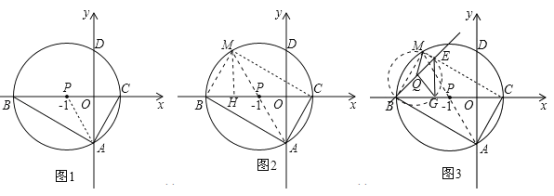
��1����B��C��������ꣻ
��2������ͼ�л����߶�MB��MC�����ж��ı���ACMB����״������֤�����������M�����ꣻ
��3����ֱ��l����BM�غϵ�λ�ÿ�ʼ�Ƶ�B˳ʱ����ת������BC�غ�ʱֹͣ����ֱ��l��CM����ΪE����QΪBE���е㣬����E��EG��BC��G������MQ��QG����������ת�����С�MQG�Ĵ�С�Ƿ�仯�������䣬�����MQG�Ķ��������仯����˵�����ɣ�
���𰸡���1��B����3��0����C��1��0������2�����Σ�M������Ϊ����2��![]() ������3������ת��������MQG�Ĵ�С���䣬ʼ�յ���120����
������3������ת��������MQG�Ĵ�С���䣬ʼ�յ���120����
�������������������1������PA�����ô������������ɶ����������Բ�İ뾶���Ӷ��������B��C��������꣮
��2������ԲP�����ĶԳ�ͼ�Σ���Ȼ����AP��ԲP�Ľ���������軭�ĵ�M������MB��MC���ɣ���֤�ı���ACMB�Ǿ��Σ�����M��MH��BC������ΪH����֤��MHP�ա�AOP���Ӷ����MH��OH�ij��������õ���M�����꣮
��3����֤��E��M��B��G���Ե�QΪԲ�ģ�QBΪ�뾶��Բ�ϣ��Ӷ��õ���MQG=2��MBG������OCA=60�����Ӷ��õ���MBG=60���������õ���MQG=120����������MQG�Ƕ�ֵ��
����������⣺��1������PA����ͼ1��ʾ����PO��AD����AO=DO����AD=![]() ����OA=
����OA=![]() ������P��������1��0������OP=1����PA=
������P��������1��0������OP=1����PA=![]() =2����BP=CP=2����B����3��0����C��1��0����
=2����BP=CP=2����B����3��0����C��1��0����
��2������AP���ӳ�AP����P�ڵ�M������MB��MC����ͼ2��ʾ���߶�MB��MC��Ϊ���������ı���ACMB�Ǿ��Σ��������£�
�ߡ�MCB����ABC�Ƶ�P��ת180�����ã����ı���ACMB��ƽ���ı��Σ�
��BC����P��ֱ�������CAB=90������ƽ���ı���ACMB�Ǿ��Σ�
����M��MH��BC������ΪH����ͼ2��ʾ��
����MHP����AOP�У��ߡ�MHP=��AOP����HPM=��OPA��MP=AP�����MHP�ա�AOP����MH=OA=![]() ��PH=PO=1����OH=2������M������Ϊ����2��
��PH=PO=1����OH=2������M����������2��![]() ����
����
��3������ת��������MQG�Ĵ�С���䣮
���ı���ACMB�Ǿ��Σ����BMC=90������EG��BO�����BGE=90�������BMC=��BGE=90����
����Q��BE���е㣬��QM=QE=QB=QG������E��M��B��G���Ե�QΪԲ�ģ�QBΪ�뾶��Բ�ϣ���ͼ3��ʾ�����MQG=2��MBG���ߡ�COA=90����OC=1��OA=![]() ����tan��OCA=
����tan��OCA=![]() =
=![]() �����OCA=60�������MBC=��BCA=60�������MQG=120����������ת��������MQG�Ĵ�С���䣬ʼ�յ���120����
�����OCA=60�������MBC=��BCA=60�������MQG=120����������ת��������MQG�Ĵ�С���䣬ʼ�յ���120����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E��F��BC�ϣ�BE=CF����A=��D����B=��C��AF��DE���ڵ�O��

��1����֤��AB=DC��
��2�����ж���OEF����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��AB��AC��ABΪ��O��ֱ����AC��BC�ֱ���O��E��D������ED��BE��

��1�����ж�DE��BD�Ƿ���ȣ���˵�����ɣ�
��2�����BC��6��AB��5����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y=��3���У�x�����������ǣ� ��
A.һ��������
B.һ��������
C.����������
D.����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=8��BC=16��������ABCD��EF�۵���ʹ��C���A�غϣ����ۺ�EF�ij�Ϊ�� ��
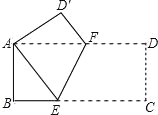
A��6 B��12 C��2![]() D��4
D��4![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��BDΪ��ABC�Ľ�ƽ���ߣ���BD=BC��EΪBD�ӳ����ϵ�һ�㣬BE=BA�����н��ۣ��١�ABD�ա�EBC����AC=2CD����AD=AE=EC���ܡ�BCE+��BCD=180����������ȷ����

A. �٢ڢ� B. �٢ڢ� C. �٢ۢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����¹���0��˵������0���෴����0�ľ���ֵ����0����0�ĵ�����0����0��ȥһ������������������෴������0�����κ��������Ե�0������˵����ȷ���У� ����
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���![]()
��1����֤������![]() ȡ�κ�ʵ��ʱ�����̺���ʵ������
ȡ�κ�ʵ��ʱ�����̺���ʵ������
��2��������![]() �Ķ��κ���
�Ķ��κ���![]() ��ͼ����
��ͼ����![]() ����������ĺ������Ϊ��������m������ֵ.
����������ĺ������Ϊ��������m������ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com