
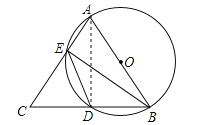
【题目】如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连结ED、BE.

(1)试判断DE与BD是否相等,并说明理由;
(2)如果BC=6,AB=5,求BE的长.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)可通过连接AD,AD就是等腰三角形ABC底边上的高,根据等腰三角形三线合一的特点,可得出∠CAD=∠BAD,根据圆周角定理即可得出∠DEB=∠DBE,便可证得DE=DB.
(2)本题中由于BE⊥AC,那么BE就是三角形ABC中AC边上的高,可用面积的不同表示方法得出ACBE=CBAD.进而求出BE的长.
试题解析:(1)DE=BD;连接AD,则AD⊥BC,在等腰三角形ABC中,AD⊥BC,∴∠CAD=∠BAD(等腰三角形三线合一),∴![]() ,∴DE=BD;
,∴DE=BD;
(2)∵AB=5,BD=![]() BC=3,∴AD=4,∵AB=AC=5,∴ACBE=CBAD,∴BE=4.8.
BC=3,∴AD=4,∵AB=AC=5,∴ACBE=CBAD,∴BE=4.8.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商店经销一批衬衣,每件进价为a元,零售价比进价高m%,后因市场变化,该商把零售价调整为原来零售价的n%出售.那么调整后每件衬衣的零售价是( )
A.a(1+m%)(1﹣n%)元
B.am%(1﹣n%)元
C.a(1+m%)n%元
D.a(1+m%n%)元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上, 顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为__ _.

查看答案和解析>>
科目:初中数学 来源: 题型:
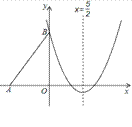
【题目】如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线![]() 经过点B,且顶点在直线
经过点B,且顶点在直线![]() 上.
上.
(1)求抛物线对应的函数关系式;
(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=![]() ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB.

(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数![]() 和一次函数
和一次函数![]() ,把
,把![]()
![]() 称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(﹣1,n),请完成下列任务:
称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(﹣1,n),请完成下列任务:
【尝试】(1)当t=2时,抛物线![]()
![]() 的顶点坐标为 ;
的顶点坐标为 ;
(2)判断点A (填是或否)在抛物线L上;
(3)n的值是 ;
【发现】通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线L总过定点,坐标为 .
【应用】二次函数![]() 是二次函数
是二次函数![]() 和一次函数
和一次函数![]() 的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com