
【题目】已知:在平面直角坐标系中,抛物线 ![]() 交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.
交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.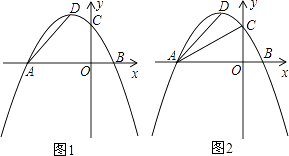
(1)求抛物线的解析式及顶点D的坐标.
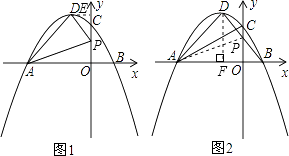
(2)如图1,当0≤t≤4时,设△PAD的面积为S,求出S与t之间的函数关系式;S是否有最小值?如果有,求出S的最小值和此时t的值.
(3)如图2,当点P运动到使∠PDA=90°时,Rt△ADP与Rt△AOC是否相似?若相似,求出点P的坐标;若不相似,说明理由.
【答案】
(1)
解:对称轴为x=﹣ ![]() =﹣2,
=﹣2,
解得b=﹣1,
所以,抛物线的解析式为y=﹣ ![]() x2﹣x+3,
x2﹣x+3,
∵y=﹣ ![]() x2﹣x+3=﹣
x2﹣x+3=﹣ ![]() (x+2)2+4,
(x+2)2+4,
∴顶点D的坐标为(﹣2,4)
(2)
解:令y=0,则﹣ ![]() x2﹣x+3=0,
x2﹣x+3=0,
整理得,x2+4x﹣12=0,
解得x1=﹣6,x2=2,
∴点A(﹣6,0),B(2,0),
如图1,过点D作DE⊥y轴于E,
∵0≤t≤4,
∴△PAD的面积为S=S梯形AOED﹣S△AOP﹣S△PDE,
= ![]() ×(2+6)×4﹣
×(2+6)×4﹣ ![]() ×6t﹣
×6t﹣ ![]() ×2×(4﹣t),
×2×(4﹣t),
=﹣2t+12,
∵k=﹣2<0,
∴S随t的增大而减小,
∴t=4时,S有最小值,最小值为﹣2×4+12=4
(3)
解:如图2,过点D作DF⊥x轴于F,
∵A(﹣6,0),D(﹣2,4),
∴AF=﹣2﹣(﹣6)=4,
∴AF=DF,
∴△ADF是等腰直角三角形,
∴∠ADF=45°,
由二次函数对称性,∠BDF=∠ADF=45°,
∴∠PDA=90°时点P为BD与y轴的交点,
∵OF=OB=2,
∴PO为△BDF的中位线,
∴OP= ![]() DF=2,
DF=2,
∴点P的坐标为(0,2),
由勾股定理得,DP= ![]() =2
=2 ![]() ,
,
AD= ![]() AF=4
AF=4 ![]() ,
,
∴ ![]() =
= ![]() =2,
=2,
令x=0,则y=3,
∴点C的坐标为(0,3),OC=3,
∴ ![]() =
= ![]() =2,
=2,
∴ ![]() =
= ![]() ,
,
又∵∠PDA=90°,∠COA=90°,
∴Rt△ADP∽Rt△AOC
【解析】(1)根据二次函数的对称轴列式求出b的值,即可得到抛物线解析式,然后整理成顶点式形式,再写出顶点坐标即可;(2)令y=0解关于x的一元二次方程求出点A、B的坐标,过点D作DE⊥y轴于E,然后根据△PAD的面积为S=S梯形AOCE﹣S△AOP﹣S△PDE , 列式整理,然后利用一次函数的增减性确定出最小值以及t值;(3)过点D作DF⊥x轴于F,根据点A、D的坐标判断出△ADF是等腰直角三角形,然后求出∠ADF=45°,根据二次函数的对称性可得∠BDF=∠ADF=45°,从而求出∠PDA=90°时点P为BD与y轴的交点,然后求出点P的坐标,再利用勾股定理列式求出AD、PD,再根据两边对应成比例夹角相等两三角形相似判断即可.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.
(1)如图①,若α=90°,求AA′的长;
(2)如图②,若α=120°,求点O′的坐标;
(3)在(Ⅱ)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A.平均数为160
B.中位数为158
C.众数为158
D.方差为20.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=2,AB=3,把梯形ABCD分别绕直线AB,CD旋转一周,所得几何体的表面积分别为S1 , S2 , 则|S1﹣S2|=(平方单位) 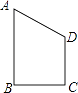
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了主题为“让勤俭节约成为时尚”的电子小组作品征集活动,现从中随机抽取部分作品,按A,B,C,D四个等级进行评价,并根据结果绘制了如下两幅不完整的统计图.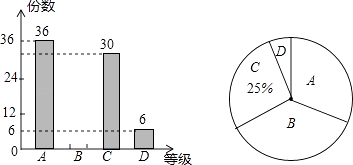
(1)求抽取了多少份作品;
(2)此次抽取的作品中等级为B的作品有 , 并补全条形统计图 ;
(3)若该校共征集到800份作品,请估计等级为A的作品约有多少份.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE= ![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是(填序号)
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是(填序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个反比例函数y= ![]() (k>1)和y=
(k>1)和y= ![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y= ![]() 的图象上,PC⊥x轴于点C,交y=
的图象上,PC⊥x轴于点C,交y= ![]() 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y= ![]() 的图象于点B,BE⊥x轴于点E,当点P在y=
的图象于点B,BE⊥x轴于点E,当点P在y= ![]() 图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是(填序号)
图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是(填序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连接这四个点,得四边形EFGH.
(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明);
(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°),
①试用含α的代数式表示∠HAE;
②求证:HE=HG;
③四边形EFGH是什么四边形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com