
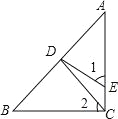
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,DE⊥AB于点D,交AC于点E.
(1)若BC=3,AC=4,求CD的长;
(2)求证:∠1=∠2.
科目:初中数学 来源: 题型:
【题目】综合题。
(1)如图,在△ABC中,AC=BC,∠ACB=90°,直线l过点C,分别过A、B两点作AD⊥l于点D,作BE⊥l于点E.求证:DE=AD+BE.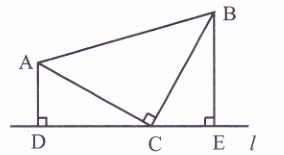
(2)如图,已知Rt△ABC,∠C=90°.用尺规作图法作出△ABC的角平分线AD;(不写作法,保留作图痕迹)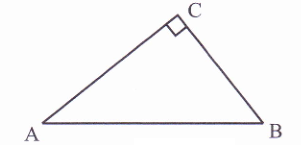
(3)若AB=10,CD=3,求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
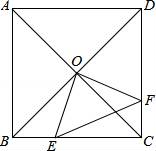
【题目】如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )
A.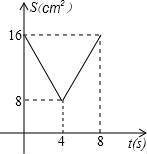
B.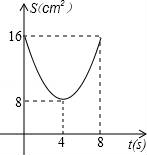
C.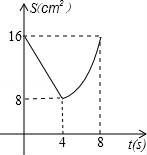
D.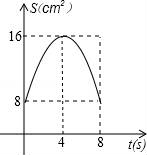
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点E为矩形ABCD边AD上一点,点P点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发t秒时,△BPQ的面积为y cm2,已知y与t的函数关系的图象如图2(曲线OM为抛物线的一部分).则下列结论:
①AE=6cm;
②当0<t≤10时,y=![]() t2;
t2;
③直线NH的解析式为y=﹣5t+110;
④若△ABE与△QBP相似,则t=![]() 秒,
秒,
其中正确结论的个数为( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寨卡病毒是一种通过蚊虫进行传播的虫媒病毒,其直径约为0.0000021cm.将数据0.0000021用科学记数法表示为( )
A.2.1×10﹣7
B.2.1×107
C.2.1×10﹣6
D.2.1×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中属于不可能事件的是( )
A. 某投篮高手投篮一次就进球
B. 打开电视机,正在播放世界杯足球比赛
C. 掷一枚骰子,向上的一面出现的点数不大于6
D. 在标准大气压下,90 ℃的水会沸腾
查看答案和解析>>
科目:初中数学 来源: 题型:
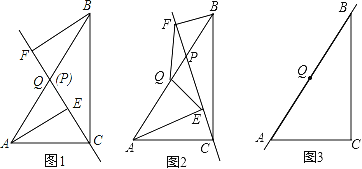
【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系式 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com