
【题目】综合题。
(1)如图,在△ABC中,AC=BC,∠ACB=90°,直线l过点C,分别过A、B两点作AD⊥l于点D,作BE⊥l于点E.求证:DE=AD+BE.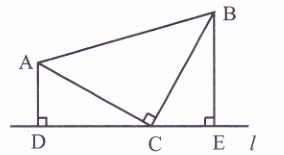
(2)如图,已知Rt△ABC,∠C=90°.用尺规作图法作出△ABC的角平分线AD;(不写作法,保留作图痕迹)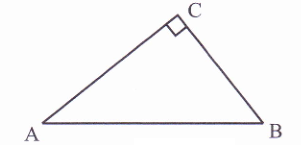
(3)若AB=10,CD=3,求△ABD的面积.
【答案】
(1)
证明:∵∠ACB=90
∴∠ACD+∠BCE=90
∵ AD⊥l
∴∠ACD+∠CAD=90
∴∠CAD=∠BCE
∵BE⊥l,AD⊥l
∴∠ADC=∠BEC=90
∵AC=BC
∴△ACD≌△CBE
∴AD=CE,CD=BE
∵DE= CD+ CE
∴DE=AD+BE.
(2)
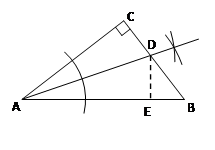
(3)
解:过点D作DE⊥AB于E

∵DC⊥AC,DE⊥AB
∴DE=DC=3
∴ ![]()
【解析】(1)根据“同角的余角相等”可证得∠CAD=∠BCE,再由AC=BC,∠ADC=∠BEC=90,可证明△ACD≌△CBE,则DE=AD+BE=CD+ CE.(2)角平分线的尺规作图方法,过A画弧交角两边的两点,再分别这两点为圆心画两条弧交于一点,连接A与这一点,交BC于点D,即AD为该角的角平分线;(3)由角平分线的性质,可作DE⊥AB于E,DE=DC=3,则可求三角形ABD的面积.


科目:初中数学 来源: 题型:
【题目】在⊙O中,AB为直径,C为⊙O上一点.
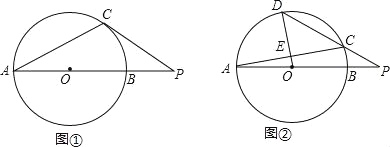
(Ⅰ)如图1.过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,求∠P的大小;
(Ⅱ)如图2,D为![]() 上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,若∠CAB=10°,求∠P的大小.
上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,若∠CAB=10°,求∠P的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=x2平移得到抛物线y=x2+5,下列叙述正确的是( )
A.向上平移5个单位
B.向下平移5个单位
C.向左平移5个单位
D.向右平移5个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.(1)求BD的长;
(2)求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一大一小的两个可以自由转动的转盘,甲盘被平均分成6等份,乙盘被平均分成4等份,每个转盘均被涂上红、黄、蓝三种颜色.转动转盘,当转盘停止后,指针指向的颜色即为转出的颜色.小明与小颖参与游戏:小明转动甲盘,小颖转动乙盘.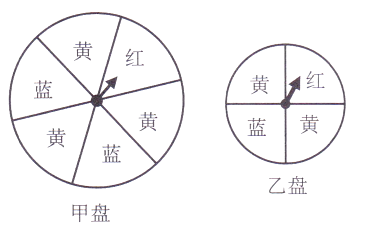
(1)小明转出的颜色为红色的概率为;
(2)小明转出的颜色为黄色的概率为;
(3)小颖转出的颜色为黄色的概率为;
(4)两人均转动转盘,如果转出的颜色为红,则胜出.你认为该游戏公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)已知点D是![]() 边AB上一动点(不与A,B重合)分别过点A,B向直线CD作垂线,垂足分别为E,F,O为边AB的中点.
边AB上一动点(不与A,B重合)分别过点A,B向直线CD作垂线,垂足分别为E,F,O为边AB的中点.
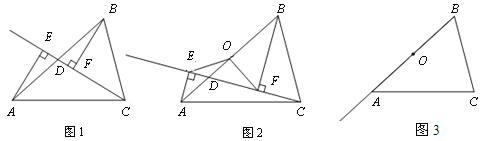
(1)如图1,当点D与点O重合时,AE与BF的位置关系是____________,OE与OF的数量关系是__________;
(2)如图2,当点D在线段AB上不与点O重合时,试判断OE与OF的数量关系,并给予证明;
(3)如图3,当点D在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并写出主要证明思路. (备注:直角三角形中,斜边上的中线等于斜边的一半)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
A.y=﹣(x﹣1)2﹣3B.y=﹣(x+1)2﹣3
C.y=﹣(x﹣1)2+3D.y=﹣(x+1)2+3
查看答案和解析>>
科目:初中数学 来源: 题型:
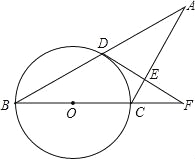
【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:
(1)AD=BD;
(2)DF是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
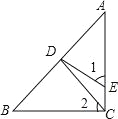
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,DE⊥AB于点D,交AC于点E.
(1)若BC=3,AC=4,求CD的长;
(2)求证:∠1=∠2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com