
【题目】如图,已知:![]() ,
,![]() .
.

(1)请找出图中一对全等的三角形,并说明理由;
(2)若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)△OAD≌△OBC,证明见解析;(2)∠BED=40°
【解析】
(1)由SAS可以判定△OAD≌△OBC
(2)△OAD≌△OBC可得∠D=∠C=25°利用三角形内角和为180°可得∠OBC=65°利用三角形的外角等于与它不相邻的两个内角的和,可得∠BED的度数.
解(1)△OAD≌△OBC
理由:在△OAD与△OBC中
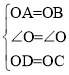
∴△OAD≌△OBC(SAS)
(2)由(1)可知:△OAD≌△OBC
∴∠D=∠C
∵∠C=25°
∴∠D=25°
∵∠O=90°
∴∠OBC=180°-∠O-∠C
=180°-90°-25°
=65°
在△BDE中,∠OBC=∠D+∠BED
∴∠BED=∠OBC-∠D
=65°-25°
=40°


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在某海域,一般指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A的救援?(参考数据:![]() ,
,![]() ,
,![]() 结果精确到0.1小时)
结果精确到0.1小时)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将三角形ABC水平向右平移得到三角形DEF,A,D两点的距离为1,CE=2,∠A=70°.根据题意完成下列各题:
(1)AC和DF的数量关系为 ;AC和DF的位置关系为 ;
(2)∠1= 度;
(3)BF= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位画家有若干个边长为![]() 的正方体,他在地面上把它们摆成如图(三层)的形式,然后,他把露出的表面都涂上颜色.
的正方体,他在地面上把它们摆成如图(三层)的形式,然后,他把露出的表面都涂上颜色.
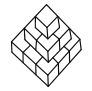
(1)图中的正方体一共有多少个?
(2)一点颜色都没涂上颜色的正方体有多少个?
(3)如果画家按此方式摆成七层,那又要多少个正方体?同样涂上颜色,又有多少个正方体没有涂上一点颜色?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识改变世界,科技改变生活.导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地13千米,导航显示车辆应沿北偏东60°方向行驶至B地,再沿北偏西37°方向行驶一段距离才能到达C地,求B、C两地的距离.(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
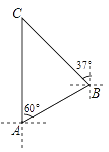
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】传统的端午节即将来临,某企业接到一批粽子生产任务,约定这批粽子的出厂价为每只4元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足如下关系:
y=![]()
(1)李明第几天生产的粽子数量为280只?
(2)如图,设第x天生产的每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价-成本)
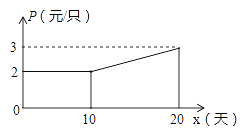
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给出五个等量关系:①AD=BC;②AC=BD;③CE=DE;④∠D=∠C;⑤∠DAB=∠CBA.
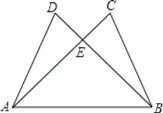
请你以其中两个为条件,另外三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.
已知:
求证:
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=![]() x+2与x轴交于点A,与y轴交于点C,抛物线y=
x+2与x轴交于点A,与y轴交于点C,抛物线y=![]() x2+bx+c经过A、C两点,与x轴的另一交点为点B.
x2+bx+c经过A、C两点,与x轴的另一交点为点B.

(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点;
①连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S1, △BCE的面积为S2, 求![]() 的最大值;
的最大值;
②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com