
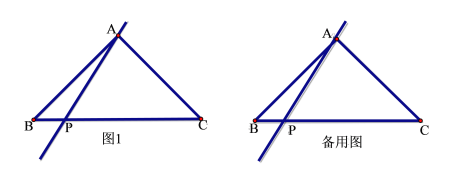
【题目】如图,△ABC中,![]() ,AB=AC,P是线段BC上一点,且
,AB=AC,P是线段BC上一点,且![]() .作点B关于直线AP的对称点D, 连结BD,CD,AD.
.作点B关于直线AP的对称点D, 连结BD,CD,AD.
(1)补全图形.
(2)设∠BAP的大小为α.求∠ADC的大小(用含α的代数式表示).
(3)延长CD与AP交于点E,直接用等式表示线段BD与DE之间的数量关系.
【答案】(1)见解析;(2)∠ADC=![]() ;(3)
;(3)![]()
【解析】
(1)根据题意画出图形即可;
(2)根据对称的性质,等腰三角形的性质及角与角之间的和差关系进行计算即可;
(3)画出图形,结合(2)的结论证明△BED为等腰直角三角形,从而得出结论.
解:(1)如图所示;

(2)∵点B与点D关于直线AP对称,∠BAP=α,
∴∠PAD=α,AB=AD,
∵![]() ,
,
∴![]() ,
,
又∵AB=AC,
∴AD=AC,
∴∠ADC=![]() =
=![]() ;
;
(3)如图,连接BE,

由(2)知:∠ADC=![]() ,
,
∵∠ADC=∠AED+∠EAD,且∠EAD=α,
∴∠AED=45°,
∵点B与点D关于直线AP对称,即AP垂直平分BD,
∴∠AED=∠AEB=45°,BE=DE,
∴∠BED=90°,
∴△BED是等腰直角三角形,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A在x轴的正半轴上,点B的坐标为(0,4),BC平分∠ABO交x轴于点C(2,0).点P是线段AB上一个动点(点P不与点A,B重合),过点P作AB的垂线分别与x轴交于点D,与y轴交于点E,DF平分∠PDO交y轴于点F.设点D的横坐标为t.
(1)如图1,当0<t<2时,求证:DF∥CB;
(2)当t<0时,在图2中补全图形,判断直线DF与CB的位置关系,并证明你的结论;
(3)若点M的坐标为(4,-1),在点P运动的过程中,当△MCE的面积等于△BCO面积的![]() 倍时,直接写出此时点E的坐标.
倍时,直接写出此时点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的一条弦,DB切⊙O于点B,过点D作DC⊥OA于点C,DC与AB相交于点E.
(1)求证:DB=DE;
(2)若∠BDE=70°,求∠AOB的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明选择一家酒店订春节团圆饭.他借助网络评价,选择了A、B、C三家酒店,对每家酒店随机选择1000条网络评价统计如下:
评价条数 等级 酒店 | 五星 | 四星 | 三星及三星以下 | 合计 |
A | 412 | 388 |
| 1000 |
B | 420 | 390 | 190 | 1000 |
C | 405 | 375 | 220 | 1000 |
(1)求x值.
(2)当客户给出评价不低于四星时,称客户获得良好用餐体验.
①请你为小明从A、B、C中推荐一家酒店,使得能获得良好用餐体验可能性最大.写出你推荐的结果,并说明理由.
②如果小明选择了你推荐的酒店,是否一定能够享受到良好用餐体验?
查看答案和解析>>
科目:初中数学 来源: 题型:
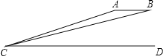
【题目】如图,某国侦察机![]() 飞抵我国近海搞侦察活动,我战斗机
飞抵我国近海搞侦察活动,我战斗机![]() 奋起拦截,地面雷达测得:当两机都处在雷达的正东方向的上空并在同一高度时,测得它们仰角分别为
奋起拦截,地面雷达测得:当两机都处在雷达的正东方向的上空并在同一高度时,测得它们仰角分别为![]() ,
,![]() ,它们与雷达的距离分别为
,它们与雷达的距离分别为![]() 千米,
千米,![]() 千米,求此时两机距离是多少千米?(精确到
千米,求此时两机距离是多少千米?(精确到![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,l1、l2、l3两两相交于A、B、C三点,它们与y轴正半轴分别交于点D、E、F,若A、B、C三点的横坐标分别为1、2、3,且OD=DE=1,则下列结论正确的个数是( )
①![]() ,②S△ABC=1,③OF=5,④点B的坐标为(2,2.5)
,②S△ABC=1,③OF=5,④点B的坐标为(2,2.5)

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1与直线![]() 交于点
交于点![]() ,直线l1分别交x轴、y轴于点A,B,OB=2,直线l2交x轴于点C.
,直线l1分别交x轴、y轴于点A,B,OB=2,直线l2交x轴于点C.

(1)求m的值及四边形OBPC的面积;
(2)求直线l1的解析式;
(3)设点Q是直线l2上的一动点,当以A、C、Q为顶点的三角形的面积等于四边形OBPC的面积时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于分别交于点
轴分别交于分别交于点![]() 、点
、点![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,两直线交于点
,两直线交于点![]() ,且
,且![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)将直线![]() 向下平移一定的距离,使得平移后的直线经过
向下平移一定的距离,使得平移后的直线经过![]() 点,且与
点,且与![]() 轴交于点
轴交于点![]() ,求四边形
,求四边形![]() 的面积.
的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com