Question

一袋装有四个上面分别标有数字1、2、3、4，除数字外其它完全相同的小球．摇匀后，甲从中任意抽取1个，记下数字后放回摇匀，乙从中任意抽一个，记下数字，然后把这两个数相加（每次抽取前均看不清小球）．
（1）请用列表或树状图的方法求两数和为3的概率；
（2）甲与乙按上述方法做游戏，当两数之和为3时，甲胜，反之乙胜．若甲胜一次得9分，那么乙胜一次得多少分，这个游戏对双方才公平？

Answer 1

【答案】分析：（1）本题考查概率问题中的公平性问题，解决本题的关键是计算出各种情况的概率，然后比较即可．
（2）根据题意可使用列表法求参与者的概率．
解答：解：（1）列表如下：

和	1	2	3	4
1	2	3	4	5
2	3	4	5	6
3	4	5	6	7
4	5	6	7	8

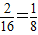
由列表可得：P（数字之和为3）=（4分）；

（2）由（1）知：P（甲胜）=，P（乙胜）=；
设乙胜一次得分应为x，才使游戏双方公平，
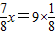
由，解得：x=，
故乙胜一次得分应为分，这个游戏对双方才公平（8分）．
点评：本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个参与者取胜的概率，概率相等就公平，否则就不公平．用到的知识点为：概率=所求情况数与总情况数之比．