
如图,正方向ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于 .
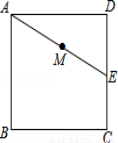
1cm或2cm.
【解析】
试题分析:根据题意画出图形,过P作PN⊥BC,交BC于点N,由ABCD为正方形,得到AD=DC=PN,在直角三角形ADE中,利用锐角三角函数定义求出DE的长,进而利用勾股定理求出AE的长,根据M为AE中点求出AM的长,利用HL得到三角形ADE与三角形PQN全等,利用全等三角形对应边,对应角相等得到DE=NQ,∠DAE=∠NPQ=30°,再由PN与DC平行,得到∠PFA=∠DEA=60°,进而得到PM垂直于AE,在直角三角形APM中,根据AM的长,利用锐角三角函数定义求出AP的长,再利用对称性确定出AP′的长即可.
试题解析:根据题意画出图形,过P作PN⊥BC,交BC于点N,
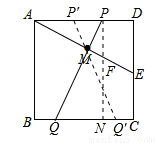
∵四边形ABCD为正方形,
∴AD=DC=PN,
在Rt△ADE中,∠DAE=30°,AD=3cm,
∴tan30°=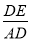
即DE=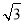 cm,
cm,
根据勾股定理得:AE=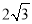 cm,
cm,
∵M为AE的中点,
∴AM=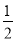 AE=
AE=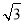 cm,
cm,
在Rt△ADE和Rt△PNQ中,
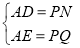 ,
,
∴Rt△ADE≌Rt△PNQ(HL),
∴DE=NQ,∠DAE=∠NPQ=30°,
∵PN∥DC,
∴∠PFA=∠DEA=60°,
∴∠PMF=90°,即PM⊥AF,
在Rt△AMP中,∠MAP=30°,cos30°=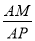 ,
,
∴AP= cm;
cm;
由对称性得到AP′=DP=AD-AP=3-2=1cm,
综上,AP等于1cm或2cm.
考点:1.全等三角形的判定与性质;2.正方形的性质;3.解直角三角形.


科目:初中数学 来源:2014-2015学年山东省九年级上学期期末调研数学试卷(解析版) 题型:解答题
(本小题满分8分)如图所示,反比例函数y1的图象经过点A(3,2),解答下列问题:
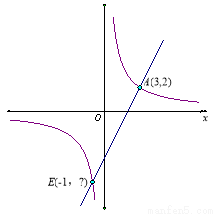
(1)求y1的函数关系式;
(2)过y1上任意一点B向x轴,y轴作垂线,交两坐标轴于C,D两点,求矩形OCBD的面积;
(3)过点A的一次函数y2与反比例函数y1的另一个交点E的横坐标为-1,求y2的关系式;
(4)通过图象回答当x取何值时,y1>y2;
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:填空题
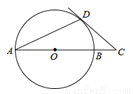
如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,连接AD.若∠A=25°,则∠C= 度.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市林甸县九年级上学期期末检测数学试卷(解析版) 题型:解答题
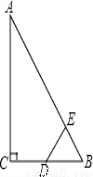
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市林甸县九年级上学期期末检测数学试卷(解析版) 题型:解答题
如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯的高度AB等于多少呢?
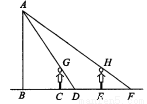
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,以O为端点画六条射线OA、OB、OC、OD、OE、OF后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线上所描的点依次记为1、2、3、4、5、6、7、8…,那么所描的第2 015个点在射线 上.
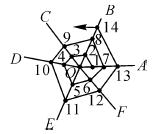
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市林甸县九年级上学期期末检测数学试卷(解析版) 题型:选择题
若A(a1,b1),B(a2,b2)是反比例函数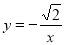 图象上的两个点,且a1<a2,则b1与b2的大小关系是 ( )
图象上的两个点,且a1<a2,则b1与b2的大小关系是 ( )
A.b1<b2 B.b1 = b2 C.b1>b2 D.大小不确定
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省长汀县城区三校九年级12月联考数学试卷(解析版) 题型:填空题
如图所示,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为_______ 。(结果保留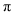 )
)
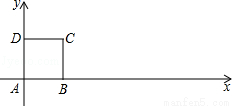
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com