
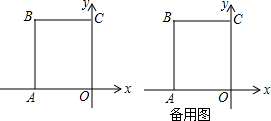
 ��ͼ����ƽ��ֱ������ϵxOy�У�A����x��ĸ������ϣ�������Ϊ��-6.0����C����y����������ϣ�������Ϊ��0��8������OA��OCΪ�ڱ��ڵڶ���������������OABC
��ͼ����ƽ��ֱ������ϵxOy�У�A����x��ĸ������ϣ�������Ϊ��-6.0����C����y����������ϣ�������Ϊ��0��8������OA��OCΪ�ڱ��ڵڶ���������������OABC���� ��1�����ݾ��ε����ʵõ�AB=OC��BC=OA����BAO=��ABC=��BCO=90�㣬���ǵõ����ۣ�
��2��������������ٵ�P��AB��ʱ���ڵ�P��AO��ʱ��������֪������ý����
��3�����������������ͼ1����P��AB��ʱ������ͼ2����P��AO��ʱ������������ACP������볤����OABC�������Ϊ1��4���з��̼��ɵõ����ۣ�
��� �⣺��1�����ı���ABCO�Ǿ��Σ�
��AB=OC��BC=OA����BAO=��ABC=��BCO=90�㣬
��A��-6.0����C��0��8����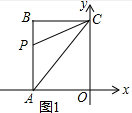
��B��-6��8����
�ʴ�Ϊ��-6��8��
��2���ٵ�P��AB��ʱ��P��-6��8-2t����
�ڵ�P��AO��ʱ��P��2t-14��0����
��3������ͼ1����P��AB��ʱ��
��������ACP������볤����OABC�������Ϊ1��4��
��$\frac{1}{2}$AP•BC=$\frac{1}{4}$AB•BC��
��$\frac{1}{2}$��8-2t����6=$\frac{1}{4}$��6��8��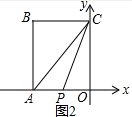
��ã�t=2��
��P��-6.4����
����ͼ2����P��AO��ʱ��
��������ACP������볤����OABC�������Ϊ1��4��
��$\frac{1}{2}$AP•AB=$\frac{1}{4}$AB•BC��
����$\frac{1}{2}$��2t-8����8=$\frac{1}{4}$��6��8��
��ã�t=$\frac{11}{2}$��
��OP=3��
��P��-3��0����
���� ���⿼����������ͼ�����ʣ��������⣬��Ҫ�����˾��ε����ʺ͵�������ȷ�����ѵ����ڣ�2��Ҫ��������ۣ�


 �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д� �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
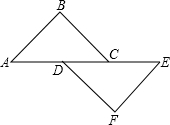 ��ͼ����ABC�ա�EFD��AB=EF��CE=2.5��CD=2����AC=��������
��ͼ����ABC�ա�EFD��AB=EF��CE=2.5��CD=2����AC=��������| A�� | 2 | B�� | 2.5 | C�� | 4 | D�� | 4.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
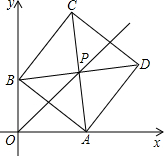 ��ƽ��ֱ������ϵxOy�У�������ABCD�ĶԽ���AC��BD�ཻ�ڵ�P������A��x�����������˶�������B��y�����������˶���x��������ᡢy��������ᶼ������ԭ��O��������C��D���ڵ�һ���ޣ���֤�����۵�A��x���������ϡ���B��y���������������˶�����P����ֱ��y=x�ϣ�
��ƽ��ֱ������ϵxOy�У�������ABCD�ĶԽ���AC��BD�ཻ�ڵ�P������A��x�����������˶�������B��y�����������˶���x��������ᡢy��������ᶼ������ԭ��O��������C��D���ڵ�һ���ޣ���֤�����۵�A��x���������ϡ���B��y���������������˶�����P����ֱ��y=x�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
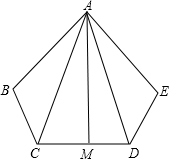 ��ͼ��AB=AE��BC=DE����B=��E��AM��CD������ΪM����֤��CM=MD��
��ͼ��AB=AE��BC=DE����B=��E��AM��CD������ΪM����֤��CM=MD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
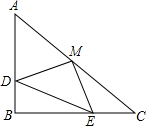 ��ͼ����֪��ABC�У���B=90�㣬AB=BC��BD=CE��M��AC���ϵ��е㣮
��ͼ����֪��ABC�У���B=90�㣬AB=BC��BD=CE��M��AC���ϵ��е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x | B�� | $\frac{1}{x}$ | C�� | $\frac{xy}{2}$ | D�� | x-3y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����ε��ڽǺ���360�� | B�� | ���ӻ�������ֱ�������� | ||
| C�� | ����һö���ӣ�6������ | D�� | 1+4��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com