
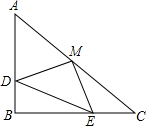
 如图,已知△ABC中,∠B=90°,AB=BC,BD=CE,M是AC边上的中点.
如图,已知△ABC中,∠B=90°,AB=BC,BD=CE,M是AC边上的中点.分析 (1)连接BM,根据△ABC中,∠B=90°,AB=BC,BD=CE,M是AC边上的中点可知BM与CM、AM的关系,BM⊥AC,从而可以推出△DBM≌△ECM,从而可以推出△DEM是等腰直角三角形.
(2)根据∠B=90°,AB=BC,BD=CE,AD=4,CE=3,可知BD=3,BE=4,从而可以得到DE的长.
解答 (1)证明:连接BM,如下图所示,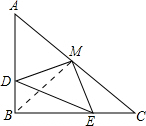
∵△ABC中,∠B=90°,AB=BC,BD=CE,M是AC边上的中点.
∴BM=AM=MC,BM⊥AC,∠A=∠DBM=∠C=45°,∠BMC=90°,
在△DBM和△ECM中,
$\left\{\begin{array}{l}{BD=CE}\\{∠DBM=∠ECM}\\{BM=CM}\end{array}\right.$,
∴△DBM≌△ECM(SAS).
∴DM=EM,∠BMD=∠CME.
∵∠BME+∠EMC=∠BMC=90°,
∴∠BMD+∠BME=90°.
∴△DME是等腰直角三角形.
(2)∵AB=BC,BD=CE,
∴AD=BE.
∵AD=4,CE=3,∠B=90°,
∴BD=3,BE=4.
∴DE=$\sqrt{B{D}^{2}+B{E}^{2}}=\sqrt{{3}^{2}+{4}^{2}}=5$.
即DE的长为5.
点评 本题考查全等三角形的判定与性质、等腰直角三角形的性质、勾股定理,解题的关键是找出所求结论或者问题需要的条件.


科目:初中数学 来源: 题型:解答题
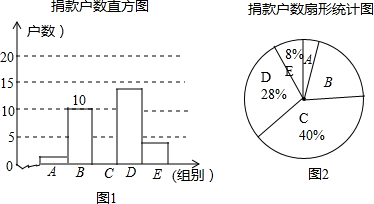 我市政府积极组织社区居民为希望工程捐款,为了解阳光社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图所示的不完整统计图.已知A、B两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题
我市政府积极组织社区居民为希望工程捐款,为了解阳光社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图所示的不完整统计图.已知A、B两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题| 组别 | 捐款额(x)元 |
| A | 10≤x<100 |
| B | 100≤x<200 |
| C | 200≤x<300 |
| D | 300≤x<400 |
| E | x≥400 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
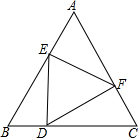 如图,△ABC是边长为9cm的等边三角形,D、E是边BC、BA上的动点,D点由B点开始以1cm/秒的速度向C点运动,E点由B点开始以2cm/秒的速度向A点运动,D、E同时出发.设运动时间为t,当其中一点到达边的端点时,运动便停止,在运动过程中始终保持∠EDF=60°.
如图,△ABC是边长为9cm的等边三角形,D、E是边BC、BA上的动点,D点由B点开始以1cm/秒的速度向C点运动,E点由B点开始以2cm/秒的速度向A点运动,D、E同时出发.设运动时间为t,当其中一点到达边的端点时,运动便停止,在运动过程中始终保持∠EDF=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
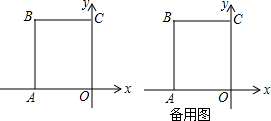 如图,在平面直角坐标系xOy中,A点在x轴的负半轴上,其坐标为(-6.0),C点在y轴的正半轴上,其坐标为(0,8),以OA,OC为邻边在第二象限内作长方形OABC
如图,在平面直角坐标系xOy中,A点在x轴的负半轴上,其坐标为(-6.0),C点在y轴的正半轴上,其坐标为(0,8),以OA,OC为邻边在第二象限内作长方形OABC查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{0.5}$ | B. | $\sqrt{{a}^{2}+{b}^{2}}$ | C. | $\frac{1}{\sqrt{5}}$ | D. | $\sqrt{50}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 150元 | B. | 160元 | C. | 170元 | D. | 180元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com