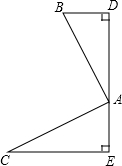
(1)解:BD=AE,AD=CE.
理由:∵BD⊥AE于D,CE⊥AE于E,∠BAC=90°,
∴∠BDA=∠AEC=90°,∠DBA+∠BAD=90°,∠BAD+∠EAC=90°,
∴∠DBA=∠EAC,
在△ABD和△CAE中,
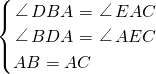
,
∴△ABD≌△CAE(AAS)
∴AD=CE,
∴DE=CE+AE=8;
(2)证明:由(1)知△ABD≌△CAE,则∠B=∠CAE.
∵∠B+∠BAD=90°,
∴∠CAE+∠BAD=90°,
∴∠CAB=90°.
分析:(1)利用AAS判定△ABD≌△CAE,根据全等三角形的对应边相等可以求得AD=CE,则DE=CE+AE;
(2)利用(1)中的全等三角形的对应角相等得到∠B=∠CAE.因为∠B+∠BAD=90°,所以∠CAE+∠BAD=90°,则∠CAB=90°.
点评:本题考查三角形全等的判定与性质,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

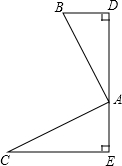 如图,已知AB=AC,BD⊥DE于D,CE⊥DE于E,BD=AE=3,CE=5.
如图,已知AB=AC,BD⊥DE于D,CE⊥DE于E,BD=AE=3,CE=5. (1)解:BD=AE,AD=CE.
(1)解:BD=AE,AD=CE.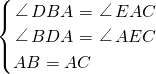 ,
,

 阅读快车系列答案
阅读快车系列答案