
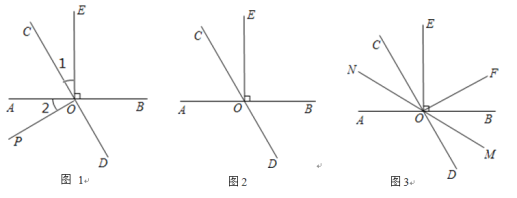
【题目】已知:直线 AB与直线 CD交于点 O,过点 O作 OE⊥AB.
①如图 1,OP 为∠AOD 内的一条射线,若∠1=∠2,求证:OP⊥CD;
②如图 2,若∠BOC=2∠AOC,求∠COE 的度数;
③如图 3.在(2)的条件下,过点 O 作 OF⊥CD,经过点 O 画直线 MN,若射线 OM平分∠BOD,请直接写出图中与 2∠EOF 度数相等的角.
【答案】①见解析;②∠COE=![]() ;③∠AOD、∠BOC、∠FON、∠EOM
;③∠AOD、∠BOC、∠FON、∠EOM
【解析】
①直接根据等量代换即可证明.
②先根据平角的定义可得∠AOC=![]() ,再利用垂直的定义可得∠AOE=
,再利用垂直的定义可得∠AOE=![]() ,从而得出结论.
,从而得出结论.
③根据②中∠AOC=![]() ,分别计算各角的度数,得其中∠EOF=
,分别计算各角的度数,得其中∠EOF=![]() ,根据各角的度数可得结论.
,根据各角的度数可得结论.
解:①∵OE⊥AB
∴∠AOC+∠1=![]()
∵∠1=∠2
∴∠AOC+∠2=![]()
∴OP⊥CD
②∵∠AOC+∠BOC=![]() ,且∠BOC=2∠AOC
,且∠BOC=2∠AOC
∴∠AOC=![]()
∵OE⊥AB
∴∠AOE=![]()
∴∠COE=![]() -
-![]() =
=![]()
③由②知:∠AOC=![]()
∵射线 OM平分∠BOD
∴∠BOM=∠DOM=∠AON=∠CON=![]()
∵OE⊥AB,OC⊥OF
∴∠AOE=∠COF=![]()
∴∠AOC=∠EOF=![]()
∴∠AOD=∠BOC=∠FON=∠EOM=![]() =2∠EOF
=2∠EOF
∴与2∠EOF度数相等的角是:∠AOD、∠BOC、∠FON、∠EOM.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】(1)请用两种不同的方法列代数式表示图1中阴影部分的面积.

方法①: ;
方法②: ;
(2)根据(1)写出一个等式: ;
(3)若x+y=8,xy=3.75,利用(2)中的结论,求x,y;
(4)有许多代数恒等式可以用图形的面积来表示.如图2,它表示了(2m+n)(m+n)=2m2+3mn+n2.试画出一个几何图形,使它的面积能表示(2m+n)(m+2n)=2m2+5mn+2n2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)一个两位数十位数字为2,则从中,2、3、4、5、6、7、8、9中任选一个数作为个位数字组成两位数,组成的两位数中是质数的概率为多少?
(2)定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“V数”,如“837”就是一个“V数”,若十位上的数字3,则从2、4、5、6中任选两数.能与3组成“V数”的概率是多少?(请用列表法或树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店销售功能相同的A、B两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器超出5个的部分按原价的七折销售,设购买x个A品牌的计算器需要y1元,购买x(x>5)个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)当需要购买50个计算器时,买哪种品牌的计算器更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
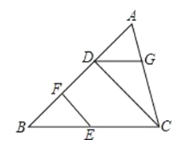
【题目】如图,已知 CD⊥AB,EF⊥AB,垂足分别为D,F,∠B+∠BDG=180°, 试说明∠BEF=∠CDG.将下面的解答过程补充完整,并填空(填写理由依据或数学式, 将答案按序号填在答题卷的对应位置内)
证明:∵CD⊥AB,EF⊥AB( ① )
∴∠BFE=∠BDC=90°( ② )
∴EF∥CD( ③ )
∴∠BEF= ④ ( ⑤ )
又∵∠B+∠BDG=180°( ⑥ )
∴BC∥DG( ⑦ )
∴∠CDG= ⑧ ( ⑨ )
∴∠CDG=∠BEF( ⑩ )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气象站观察一场沙尘暴从发生到结束的全过程,开始时风速按一定的速度匀速增大,经过荒漠地时,风速增大的比较快.一段时间后,风速保持不变,当沙尘暴经过防风林时,其风速开始逐渐减小,最终停止.如图所示是风速与时间之间的关系的图象.结合图象回答下列问题:

(1)沙尘暴从开始发生到结束共经历了多长时间?
(2)从图象上看,风速在哪一个时间段增大的比较快,增加的速度是多少?
(3)风速在哪一时间段保持不变,经历了多长时间?
(4)风速从开始减小到最终停止,风速每小时减小多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读探究:12=![]() ,12+22=
,12+22=![]() ,12+22+32=
,12+22+32=![]() ,…
,…
(1)根据上述规律,求12+22+32+42+52的值;
(2)你能用一个含有n(n为正整数)的算式表示这个规律吗?请直接写出这个算式(不计算);
(3)根据你发现的规律,计算下面算式的值:62+72+82+92+102+112+122+132+142+152.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论::①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是 . (请写出正确结论的序号).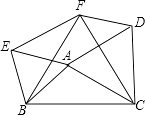
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的![]() 时,求出这时点M的坐标.
时,求出这时点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com