【题目】阅读探究：12=
，12+22=
，12+22+32=
，…
（1）根据上述规律，求12+22+32+42+52的值；
（2）你能用一个含有n（n为正整数）的算式表示这个规律吗？请直接写出这个算式（不计算）；
（3）根据你发现的规律，计算下面算式的值：62+72+82+92+102+112+122+132+142+152．
【答案】（1）55；（2）12+22+32+…+n2 =
（n为正整数）；（3）1185．
【解析】
（1）观察不难发现，从1开始的平方数的和，分母都是6，分子为最后一个数与比它大1的数的积再乘以比这个数的2倍大1的数的积；
（2）根据规律写出即可；
（3）用前15个数的平方和减去前5个数的平方和，列式计算即可得解．
解：（1）根据题意得：原式=
=55；
（2）根据题意得：12+22+32+…+n2 =（n为正整数）；
（3）根据题意得：12+22+32+42+52 = 55①，
12+22+32+42+52+62+72+82+92+102+112+122+132+142+152=
=1240②，
由②﹣①得：62+72+82+92+102+112+122+132+142+152=1185．
科目：初中数学 来源： 题型：
【题目】“C919”大型客机首飞成功，激发了同学们对航空科技的兴趣，如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸，图中AB∥CD，AM∥BN∥ED，AE⊥DE，请根据图中数据，求出线段BE和CD的长．（sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，结果保留小数点后一位）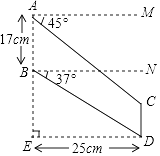
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列算式：
第1个式子： 
第2个式子： 
第3个式子： 
第4个式子： 
（1）可猜想第7个等式为 ．
（2）探索规律，若字母
表示自然数，请写出第个等式 ．
（3）试证明你写出的等式的正确性．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：直线 AB与直线 CD交于点 O，过点 O作 OE⊥AB．
①如图 1，OP 为∠AOD 内的一条射线，若∠1＝∠2，求证：OP⊥CD；
②如图 2，若∠BOC＝2∠AOC，求∠COE 的度数；
③如图 3．在（2）的条件下，过点 O 作 OF⊥CD，经过点 O 画直线 MN，若射线 OM平分∠BOD，请直接写出图中与 2∠EOF 度数相等的角．
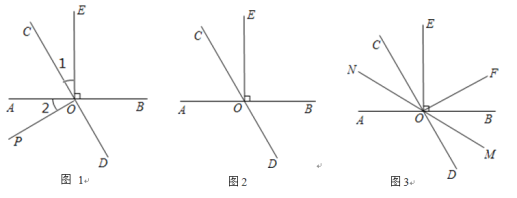
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线
，直线
与直线
、
分别相交于点
、
．
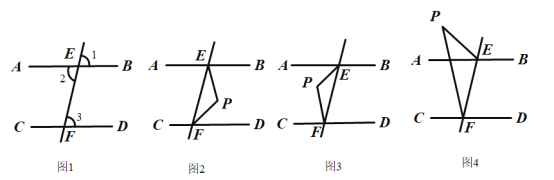
（1）如图1，若
，求
，
的度数；
（2）若点
是平面内的一个动点，连接
、
，探索
、
、
之间的数量关系；
①当点在图2的位置时，请写出、、之间的数量关系并证明；
②当点在图3的位置时，请写出、、之间的数量关系并证明；
③当点在图4的位置时，请直接写出、、之间的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
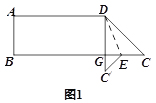
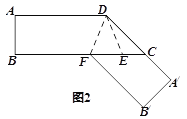
【题目】已知四边形ABCD，其中AD//BC，AB⊥BC，将DC沿DE折叠，C落于
，
交CB于G，且ABGD为长方形（如图1）；再将纸片展开，将AD沿DF折叠，使A点落在DC上一点
（如图2），在两次折叠过程中，两条折痕DE、DF所成的角为____________度.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是抛物线y1=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：
①2a+b=0；
②abc＞0；
③方程ax2+bx+c=3有两个相等的实数根；
④抛物线与x轴的另一个交点是（﹣1，0）；
⑤当1＜x＜4时，有y2＜y1 ，
其中正确的是（ ）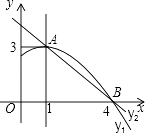
A.①②③
B.①③④
C.①③⑤
D.②④⑤
查看答案和解析>>
科目：初中数学 来源： 题型：
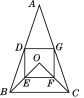
【题目】如图，在△ABC中，AB＝AC，点O在△ABC的内部，∠BOC＝90°，OB＝OC，D，E，F，G分别是AB，OB，OC，AC的中点．
(1)求证：四边形DEFG是矩形；
(2)若DE＝2，EF＝3，求△ABC的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
