
【题目】如图,在四边形ABCD中,AB=AD=4,∠A=60°,BC=4 ![]() ,CD=8.
,CD=8. 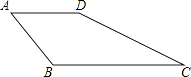
(1)求∠ADC的度数;
(2)求四边形ABCD的面积.
【答案】
(1)解:连接BD,

∵AB=AD,∠A=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,DB=4,
∵42+82=(4 ![]() )2,
)2,
∴DB2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=60°+90°=150°
(2)解:过B作BE⊥AD,
∵∠A=60°,AB=4,
∴BE=ABsin60°=4× ![]() =2
=2 ![]() ,
,
∴四边形ABCD的面积为: ![]() ADEB+
ADEB+ ![]() DBCD=
DBCD= ![]() ×4×
×4× ![]() +
+ ![]() ×4×8=4
×4×8=4 ![]() +16
+16
【解析】(1)连接BD,首先证明△ABD是等边三角形,可得∠ADB=60°,DB=4,再利用勾股定理逆定理证明△BDC是直角三角形,进而可得答案;(2)过B作BE⊥AD,利用三角形函数计算出BE长,再利用△ABD的面积加上△BDC的面积可得四边形ABCD的面积.
【考点精析】关于本题考查的勾股定理的逆定理,需要了解如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形才能得出正确答案.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】不能判定两个三角形全等的条件是( )
A.三条边对应相等B.两条边及其夹角对应相等
C.两角及其中一角的对边对应相等D.两条边和一条边所对的角对应相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系和位置关系;(不要求证明)
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断予以证明;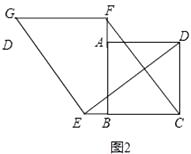
(3)如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.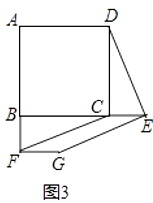
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次篮球联赛初赛阶段,每队有![]() 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得![]() 分, 负一场得
分, 负一场得![]() 分,积分超过
分,积分超过![]() 分才能获得参赛资格.
分才能获得参赛资格.
(1)已知甲队在初赛阶段的积分为![]() 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;
(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com