Question

【题目】四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF。

（1）求证：△ADE≌△ABF；

（2）填空：△ABF可以由△ADE绕旋转中心 点，按顺时针方向旋转 度得到；

（3）若BC=8，DE=6，求△AEF的面积。

Answer 1

【答案】（1）证明见解析；（2）A，90；（3）50.

【解析】试题分析：（1）根据正方形的性质得AD=AB，∠D=∠ABC=90°，然后利用“SAS”易证得△ADE≌△ABF；

（2）由于△ADE≌△ABF得∠BAF=∠DAE，则∠BAF+∠BAE=90°，即∠FAE=90°，根据旋转的定义可得到△ABF可以由△ADE绕旋转中心 A点，按顺时针方向旋转90 度得到；

（3）先利用勾股定理可计算出AE=10，再根据△ABF可以由△ADE绕旋转中心 A点，按顺时针方向旋转90 度得到AE=AF，∠EAF=90°，然后根据直角三角形的面积公式计算即可．

（1）证明：∵四边形ABCD是正方形，

∴AD=AB，∠D=∠ABC=90°，

而F是CB的延长线上的点，

∴∠ABF=90°，

在△ADE和△ABF中

，

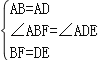∴△ADE≌△ABF（SAS）；

（2）解：∵△ADE≌△ABF，

∴∠BAF=∠DAE，

而∠DAE+∠EAB=90°，

∴∠BAF+∠EAB=90°，即∠FAE=90°，

∴△ABF可以由△ADE绕旋转中心 A点，按顺时针方向旋转90 度得到；

故答案为A、90；

（3）解：∵BC=8，

∴AD=8，

在Rt△ADE中，DE=6，AD=8，

∴AE==10，

∵△ABF可以由△ADE绕旋转中心 A点，按顺时针方向旋转90 度得到，

∴AE=AF，∠EAF=90°，

∴△AEF的面积=AE2=×100=50（平方单位）．