
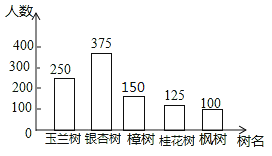
【题目】为积极响应市委政府“加快建设天蓝水碧地绿的美丽长沙”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:

请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为: ;
(2)请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民8万人,请你估计这8万人中最喜欢玉兰树的有多少人?
【答案】(1)1000;(2)图见解析;(3)36°;(4)2万.
【解析】
试题分析:(1)根据喜欢“银杏树”的人数除以其占的百分比即可得总人数;(2)用总人数减去选择其它4种树的人数可得喜欢“樟树”的人数,补全条形图即可;(3)用样本中喜欢“枫树”占总人数的比例乘以360°即可得答案;(4)用样本中最喜欢“玉兰树”的比例乘以总人数可得答案.
试题解析:(1)这次参与调查的居民人数为375÷37.5%=1000(人);
(2)选择“樟树”的有1000﹣250﹣375﹣125﹣100=150(人),
补全条形图如图:
(3)360°×![]() =36°,
=36°,
答:扇形统计图中“枫树”所在扇形的圆心角度数为36°;
(4)8×![]() =2(万人),
=2(万人),
答:估计这8万人中最喜欢玉兰树的约有2万人.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF。

(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数![]() (
(![]() 为正常数)的图象与
为正常数)的图象与![]() 轴交于A、B两点(A在B的左侧),与
轴交于A、B两点(A在B的左侧),与![]() 轴交于C点.直线
轴交于C点.直线![]() 过M(0,m)(
过M(0,m)(![]() 且
且![]() )且与x轴平行,并与直线AC、BC分别相交于点D、E.二次函数
)且与x轴平行,并与直线AC、BC分别相交于点D、E.二次函数![]() 的图象关于直线
的图象关于直线![]() 的对称图象与y轴交于点P.设直线PD与
的对称图象与y轴交于点P.设直线PD与![]() 轴交点为Q ,则:
轴交点为Q ,则:
⑴ 求A、C两点的坐标;
⑵ 求![]() 的值(用含m的代数式表示);
的值(用含m的代数式表示);
⑶ 是否存在实数m,使![]() ?若能,则求出相应的m的值;若不能,请说明理由.
?若能,则求出相应的m的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P到x轴的距离为2,到y轴的距离为3,且点P在x轴的上方,则点P的坐标为( )
A. (2,3)B. (3,2)
C. (2,3)或(-2,3)D. (3,2)或(-3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AB=14,BC=15,AC=13
(1) sinB=_________,△ABC的面积为_________
(2) 如图2,点P由B点出发,以1个单位/s的速度向C点运动,过P作PE∥AB、PD∥AC分别交AC、AB边于E、D点,设运动时间为t秒
① 是否存在唯一的t值,使四边形PEAD的面积为S?若存在,求S值;若不存在,说明理由
② 如图3,将△PDE沿DE折叠至△QDE位置,连BQ、CQ,当t为何值时,2BQ=CQ



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=![]() 和函数y=
和函数y=![]() x+1的图象交于A,B两点,点A的坐标为(2,2),以下结论:①反比例函数的图象一定过点(-1,-4);②当x>2时,
x+1的图象交于A,B两点,点A的坐标为(2,2),以下结论:①反比例函数的图象一定过点(-1,-4);②当x>2时, ![]() x+1>
x+1>![]() ;③点B的坐标是(-4,-1);④S△OCD=1,其中正确结论的个数是( )
;③点B的坐标是(-4,-1);④S△OCD=1,其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点P在x轴上,且到y轴的距离为2,则点P的坐标是( )
A. (0,2)B. (0,2)或(0,﹣2)
C. (2,0)D. (2,0)或(﹣2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某细胞截面可以近似看成圆,它的半径约为0.000 000787m,则0.000 000787用科学记数法表示为( )
A.7.87×107
B.7.87×10﹣7
C.0.787×10﹣7
D.7.87×10﹣6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com