Question

13．点D在等边三角形△ABC的边BC上，将△ABD绕点A旋转，使得旋转后点B的对应点为点C．
（1）在图1中画出旋转后的图形．
（2）小颖是这样做的：如图2，过点C画BA的平行线L，在L上取CE=BD，连接AE，则△ACE即为旋转后的图形．小颖这样做对吗？请你说说理由．

Answer 1

分析 （1）直接利用旋转的性质得出对应点位置进而得出答案；
（2）直接利用等边三角形的性质结合全等三角形的判定方法进而得出答案．

解答 解：（1）如图1所示：△ACD′即为所求；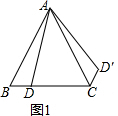

（2）小颖这样做对，
理由：如图2，∵△ABC是等边三角形，
∴AB=AC，∠B=∠ACB=60°，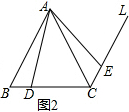
∵AB∥直线L，
∴∠B+∠BCE=180°，
∴∠ACE=60°，
在△ABD和△ACE中，
$\left\{\begin{array}{l}{AB=AC}\\{∠B=∠ACE}\\{BD=CE}\end{array}\right.$，
∴△ABD≌△ACE（SAS），
∴△ACE即为旋转后的图形．

点评 此题主要考查了旋转变换以及全等三角形的判定，正确应用等边三角形的性质是解题关键．