
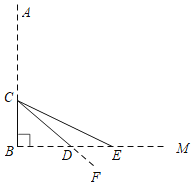
【题目】如图,池塘边一棵垂直于水面BM的笔直大树AB在点C处折断,AC部分倒下,点A与水面上的点E重合,部分沉入水中后,点A与水中的点F重合,CF交水面于点D,DF=2m,∠CEB=30°,∠CDB=45°,求CB部分的高度.(精确到0.1m.参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
科目:初中数学 来源: 题型:
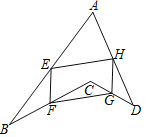
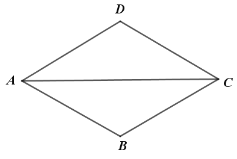
【题目】如图,在“飞镖形”ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
(1)求证:四边形EFGH是平行四边形;
(2)“飞镖形”ABCD满足条件 时,四边形EFGH是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
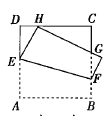
【题目】如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点AB E,交BC于点F,边AB折叠后与边BC交于点G,设正方形ABCD的周长为m,![]() 的周长为n,则
的周长为n,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.随H点位置的变化而变化
D.随H点位置的变化而变化
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是菱形,且
是菱形,且![]() ,点
,点![]() 是对角线
是对角线![]() 上一点,
上一点,![]() ,绕点
,绕点![]() 逆时针旋转射线
逆时针旋转射线![]() ,旋转角度为
,旋转角度为![]() ,并交射线
,并交射线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,
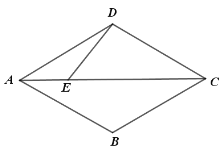
(1)①当![]() 时,补全图形,并证明
时,补全图形,并证明![]() ;
;
②当![]() 时,直接写出线段
时,直接写出线段![]() ,
,![]() ,
,![]() 之间的关系;
之间的关系;
(2)在平面上找到一点![]() ,使得对于任意的
,使得对于任意的![]() ,总有
,总有![]() ,直接写出点
,直接写出点![]() 的位置.
的位置.
(3)选择下面任意一问回答即可(全卷最多不超过100分)
A.证明(1)②的结论. | B.根据(2)中找到的 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴是直线x=﹣1,且过点(1,0).顶点位于第二象限,其部分图象如图4所示,给出以下判断:①ab>0且c<0;②4a﹣2b+c>0;③8a+c>0;④c=3a﹣3b;⑤直线y=2x+2与抛物线y=ax2+bx+c两个交点的横坐标分别为x1,x2,则x1+x2+x1x2=5.其中正确的个数有( )
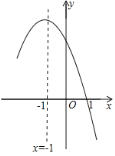
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有![]() 名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
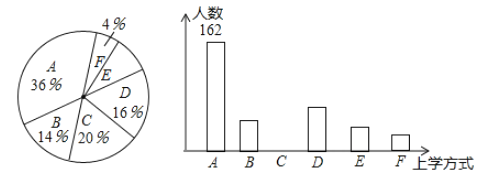
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有_____人,其中选择![]() 类的人数有_____人;
类的人数有_____人;
(2)在扇形统计图中,求![]() 类对应的扇形圆心角
类对应的扇形圆心角![]() 的度数,并补全条形统计图;
的度数,并补全条形统计图;
(3)若将![]() 这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠B=60°,AB=2,M为边AB的中点,N为边BC上一动点(不与点B重合),将△BMN沿直线MN折叠,使点B落在点E处,连接DE、CE,当△CDE为等腰三角形时,BN的长为_____.
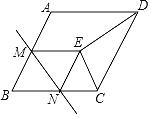
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b 的图象与反比例函数y=![]() 的图交象于A、B两点,且点A的横坐标和点B的纵坐标都是-2 , 求:
的图交象于A、B两点,且点A的横坐标和点B的纵坐标都是-2 , 求:
(1)一次函数的解析式;
(2)△AOB的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+4x+c(a≠0)的图象与x轴交A,B两点,与y轴交于点C,直线y=﹣2x﹣6经过点A,C.
(1)求该二次函数的解析式;
(2)点P为第三象限内抛物线上的一个动点,△APC的面积为S,试求S的最大值;
(3)若P为抛物线的顶点,且直角三角形APQ的直角顶点Q在y轴上,请直接写出点Q的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com