
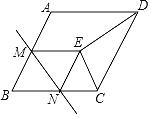
【题目】如图,在菱形ABCD中,∠B=60°,AB=2,M为边AB的中点,N为边BC上一动点(不与点B重合),将△BMN沿直线MN折叠,使点B落在点E处,连接DE、CE,当△CDE为等腰三角形时,BN的长为_____.
【答案】![]() 或2
或2
【解析】
分两种情况:①当DE=DC时,连接DM,作DG⊥BC于G,由菱形的性质得出AB=CD=BC=2,AD∥BC,AB∥CD,得出∠DCG=∠B=60°,∠A=120°,DE=AD=2,求出DG=![]() CG=
CG=![]() ,BG=BC+CG=3,由折叠的性质得EN=BN,EM=BM=AM,∠MEN=∠B=60°,证明△ADM≌△EDM,得出∠A=∠DEM=120°,证出D、E、N三点共线,设BN=EN=xcm,则GN=3-x, DN=x+2,在Rt△DGN中,由勾股定理得出方程,解方程即可;②当CE=CD上,CE=CD=AD,此时点E与A重合,N与点C重合,CE=CD=DE=DA,△CDE是等边三角形,BN=BC=2(含CE=DE这种情况);
,BG=BC+CG=3,由折叠的性质得EN=BN,EM=BM=AM,∠MEN=∠B=60°,证明△ADM≌△EDM,得出∠A=∠DEM=120°,证出D、E、N三点共线,设BN=EN=xcm,则GN=3-x, DN=x+2,在Rt△DGN中,由勾股定理得出方程,解方程即可;②当CE=CD上,CE=CD=AD,此时点E与A重合,N与点C重合,CE=CD=DE=DA,△CDE是等边三角形,BN=BC=2(含CE=DE这种情况);
解:分两种情况:
①当DE=DC时,连接DM,作DG⊥BC于G,如图1所示:
∵四边形ABCD是菱形,
∴AB=CD=BC=2,AD∥BC,AB∥CD,
∴∠DCG=∠B=60°,∠A=120°,
∴DE=AD=2,
∵DG⊥BC,
∴∠CDG=90°﹣60°=30°,
∴CG=![]() CD=1,
CD=1,
∴DG=![]() CG=
CG=![]() ,BG=BC+CG=3,
,BG=BC+CG=3,
∵M为AB的中点,
∴AM=BM=1,
由折叠的性质得:EN=BN,EM=BM=AM,∠MEN=∠B=60°,
在△ADM和△EDM中,
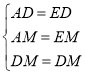 ,
,
∴△ADM≌△EDM(SSS),
∴∠A=∠DEM=120°,
∴∠MEN+∠DEM=180°,
∴D、E、N三点共线,
设BN=EN=x,则GN=3﹣x,DN=x+2,
在Rt△DGN中,由勾股定理得:(3﹣x)2+(![]() )2=(x+2)2,
)2=(x+2)2,
解得:x=![]() ,
,
即BN=![]() ,
,
②当CE=CD时,CE=CD=AD,此时点E与A重合,N与点C重合,如图2所示:
CE=CD=DE=DA,△CDE是等边三角形,BN=BC=2(含CE=DE这种情况);
综上所述,当△CDE为等腰三角形时,线段BN的长为![]() 或2;
或2;
故答案为:![]() 或2.
或2.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为直线
为直线![]() 上一点,点
上一点,点![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,连结
,连结![]() 、
、![]() 、
、![]() .
.
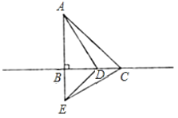
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的度数.
的度数.
(3)若点![]() 是
是![]() 的外心,当点
的外心,当点![]() 在直线
在直线![]() 的一个位置运动到另一个位置时,点
的一个位置运动到另一个位置时,点![]() 恰好在
恰好在![]() 的内部,请直接写出点
的内部,请直接写出点![]() 走过的距离为_____.
走过的距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
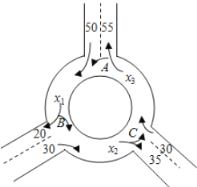
【题目】如图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出口![]() ,
,![]() ,
,![]() 的机动车辆数如图所示,图中
的机动车辆数如图所示,图中![]() ,
,![]() ,
,![]() 分别表示该时段单位时间通过路段
分别表示该时段单位时间通过路段![]() ,
,![]() ,
,![]() 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等).
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等).
(1)若![]() ,
,![]() __________.
__________.
(2)![]() 与
与![]() 的等量关系为__________.
的等量关系为__________.
(3)![]() ,
,![]() ,
,![]() 的大小关系为__________.(用>连接).
的大小关系为__________.(用>连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,池塘边一棵垂直于水面BM的笔直大树AB在点C处折断,AC部分倒下,点A与水面上的点E重合,部分沉入水中后,点A与水中的点F重合,CF交水面于点D,DF=2m,∠CEB=30°,∠CDB=45°,求CB部分的高度.(精确到0.1m.参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
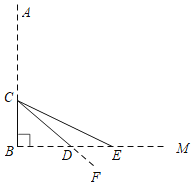
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的半径为 4,
的半径为 4,![]() 是圆的直径,点
是圆的直径,点![]() 是
是![]() 的切线
的切线![]() 上的一个动点,连接
上的一个动点,连接![]() 交
交![]() 于点
于点![]() ,弦
,弦![]() 平行于
平行于![]() ,连接
,连接![]() .
.
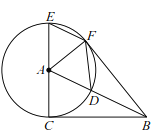
(1)试判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当![]() __________时,四边形
__________时,四边形![]() 为菱形;
为菱形;
(3)当![]() ___________时,四边形
___________时,四边形![]() 为正方形.
为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,过点
,过点![]() 作直线
作直线![]() ,将
,将![]() 绕点C顺时针旋转得到
绕点C顺时针旋转得到![]() (点
(点![]() 的对应点分别是
的对应点分别是![]() ),射线
),射线![]() 分别交直线
分别交直线![]() 于点
于点![]() .
.
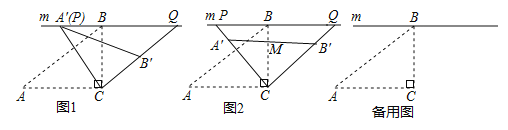
(1)问题发现:如图1所示,若![]() 与
与![]() 重合,则
重合,则![]() 的度数为_________________
的度数为_________________
(2)类比探究:如图2,所示,设![]() 与
与![]() 的交点为M,当M为
的交点为M,当M为![]() 中点时,求线段
中点时,求线段![]() 的长;
的长;
(3)拓展延伸:在旋转过程中,当点![]() 分别在
分别在![]() 的延长线上时,试探究四边形
的延长线上时,试探究四边形![]() 的面积是否存在最小值,若存在,直接写出四边形
的面积是否存在最小值,若存在,直接写出四边形![]() 的最小面积;若不存在,请说明理由
的最小面积;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师为了了解班级学生完成数学课前预习的具体情况,对本班部分学生进行了为期半个月的跟踪调查.他将调查结果分为四类:A:很好;B:较好;C:一般;D:较差,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)请计算出A类男生和C类女生的人数,并将条形统计图补充完整.
(2)为了共同进步,张老师想从被调查的A类和D类学生中各随机机抽取一位同学进行“一帮一”互助学习,请用画树状图或列表的方法求出所选两位同学恰好是一男一女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠B=90°,AB=BC=12cm,点D从点A出发沿边AB以2cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC(点E、F分别在AC、BC上).设点D移动的时间为t秒.
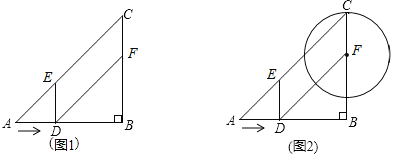
(1)试判断四边形DFCE的形状,并说明理由;
(2)当t为何值时,四边形DFCE的面积等于20cm2?
(3)如图2,以点F为圆心,FC的长为半径作⊙F,在运动过程中,当⊙F与四边形DFCE只有1个公共点时,请直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业接到一批防护服生产任务,按要求15天完成,已知这批防护服的出厂价为每件80元,为按时完成任务,该企业动员放假回家的工人及时返回加班赶制.该企业第![]() 天生产的防护服数量为
天生产的防护服数量为![]() 件,
件,![]() 与
与![]() 之间的关系可以用图中的函数图象来刻画.
之间的关系可以用图中的函数图象来刻画.

(1)直接写出![]() 与
与![]() 的函数关系式________;
的函数关系式________;
(2)由于疫情加重,原材料紧缺,防护服的成本前5天为每件50元,从第6天起每件防护服的成本比前一天增加2元,设第![]() 天创造的利润为
天创造的利润为![]() 元,直接利用(1)的结论,求
元,直接利用(1)的结论,求![]() 与
与![]() 之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)
之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com