
ΓΨΧβΡΩΓΩΫϋΤΎΘ§Έ“ –≥÷–χ≥ωœ÷Έμω≤ΧλΤχΘ§ΗχΙψ¥σ –ΟώΒΡΙΛΉςΚΆ…ζΜν‘λ≥…ΝΥ―œ÷ΊΒΡ”ΑœλΘ°ΈΣ¥ΥΘ§ΓΑΈμω≤ΧλΤχΒΡ÷ς“Σ≥…“ρΓ±ΨΆ≥…ΈΣΝΥΡ≥–ΘΜΖ±Θ–ΓΉιΒς≤ι―–ΨΩΒΡΩΈΧβΘ§ΥϊΟ«ΥφΜζΒς≤ιΝΥ≤ΩΖ÷ –ΟώΘ§≤ΔΕ‘Βς≤ιΫαΙϊΫχ––ΝΥ’ϊάμΘ§Μφ÷ΤΝΥ»γΆΦΥυ ΨΒΡ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦ±μΘ°«κΗυΨίΆΦ±μ÷–ΧαΙ©ΒΡ–≈œΔΫβ¥πœ¬Ν–Έ Χβ:
ΦΕ±π | ΙέΒψ | ΤΒ ΐΘ®»Υ ΐΘ© |
A | ¥σΤχΤχ―ΙΒΆΘ§Ω’Τχ≤ΜΝςΕ· |
|
B | ΒΊΟφΜ“≥Ψ¥σΘ§Ω’Τχ ΣΕ»ΒΆ |
|
C | Τϊ≥ΒΈ≤≤Ω≈≈Ζ≈ |
|
D | ΙΛ≥ß‘λ≥…Έέ»Ψ |
|
E | ΤδΥϊ |
|
Βς≤ιΫαΙϊ…»–ΈΆ≥ΦΤΆΦ
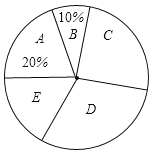
Θ®1Θ©ΧνΩ’ΘΚ![]() ______Θ§
______Θ§![]() ______ΘΜ
______ΘΜ
Θ®2Θ©«σ≥ω…»–ΈΆ≥ΦΤΆΦ÷–EΉιΥυ’ΦΒΡΑΌΖ÷±»“‘ΦΑ…»–ΈΆ≥ΦΤΆΦ÷–«χ”ρDΥυΕ‘”ΠΒΡ…»–Έ‘≤–ΡΫ«Ε» ΐΘΜ
ΓΨ¥πΑΗΓΩ(1)40;100;(2)EΥυ’ΦΑΌΖ÷±»:15%;DΥυΕ‘”Π‘≤–ΡΫ«:108Γψ.
ΓΨΫβΈωΓΩ
(1)œ»άϊ”ΟAΥψ≥ωΉή»Υ ΐ,‘Ό”ΟBΒΡΑΌΖ÷±»Υψ≥ωm,”ΟΉή»Υ ΐΦθ»ΞΖ«CΦΕ±πΒΡ»Υ ΐΥψ≥ωn.
(2)άϊ”ΟEΦΕ±πΒΡ»Υ ΐ≥ΐΉή»Υ ΐΥψ≥ωΑΌΖ÷±»;œ»Υψ≥ωDΦΕ±πΑΌΖ÷±»,‘Ό”κ360Γψœύ≥ΥΦ¥Ω…Υψ≥ω.
(1)Βς≤ιΉή»Υ ΐ:80Γ¬20%=400.
m=400ΓΝ10%=40,n=400Θ≠80Θ≠40Θ≠120Θ≠60=100.
(2)EΥυ’ΦΑΌΖ÷±»:60Γ¬400=15%.
DΥυΕ‘”ΠΒΡ…»–Έ‘≤–ΡΫ«Ε» ΐ:![]() .
.


 ÷«Ρή―ΒΝΖΝΖ≤βΩΦœΒΝ–¥πΑΗ
÷«Ρή―ΒΝΖΝΖ≤βΩΦœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓœAOB=10ΓψΘ§ΒψP‘ΎOB…œΘ°“‘ΒψPΈΣ‘≤–ΡΘ§OPΈΣΑκΨΕΜ≠ΜΓΘ§ΫΜOA”ΎΒψP1Θ®ΒψP1”κΒψO≤Μ÷ΊΚœΘ©Θ§Ν§Ϋ”PP1ΘΜ‘Ό“‘ΒψP1ΈΣ‘≤–ΡΘ§OPΈΣΑκΨΕΜ≠ΜΓΘ§ΫΜOB”ΎΒψP2Θ®ΒψP2”κΒψP≤Μ÷ΊΚœΘ©Θ§Ν§Ϋ”P1 P2ΘΜ‘Ό“‘ΒψP2ΈΣ‘≤–ΡΘ§OPΈΣΑκΨΕΜ≠ΜΓΘ§ΫΜOA”ΎΒψP3Θ®ΒψP3”κΒψP1≤Μ÷ΊΚœΘ©Θ§Ν§Ϋ”P2 P3ΘΜΓ≠Γ≠
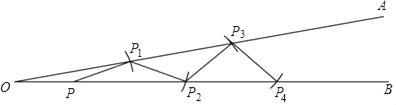
«κΑ¥’’…œΟφΒΡ“Σ«σΦΧ–χ≤ΌΉς≤ΔΧΫΨΩΘΚ
ΓœP3 P2 P4=_____ΓψΘΜΑ¥’’…œΟφΒΡ“Σ«σ“Μ÷±Μ≠œ¬»ΞΘ§ΒΟΒΫΒψPnΘ§»τ÷°ΚσΨΆ≤ΜΡή‘ΌΜ≠≥ωΖϊΚœ“Σ«σΒψPn+1ΝΥΘ§‘ρn=_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ’ΐΖΫ–ΈABCD±Ώ≥ΛΈΣ3Θ§ΒψE‘ΎAB±Ώ…œ«“BE=1Θ§ΒψPΘ§QΖ÷±π «±ΏBCΘ§CDΒΡΕ·ΒψΘ®Ψυ≤Μ”κΕΞΒψ÷ΊΚœΘ©Θ§Β±ΥΡ±Ώ–ΈAEPQΒΡ÷ή≥Λ»ΓΉν–Γ÷Β ±Θ§ΥΡ±Ώ–ΈAEPQΒΡΟφΜΐ «Θ®ΓΓΓΓΘ©
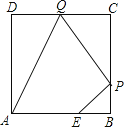
A. 3 B. 5 C. 4 D. 1
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΝβ–ΈABCD÷–Θ§ΒψEΘ§FΘ§GΘ§HΖ÷±π «±ΏABΘ§BCΘ§CDΚΆDAΒΡ÷–ΒψΘ§Ν§Ϋ”EFΘ§FGΘ§GHΚΆHEΘ§»τEH=2EF=2Θ§‘ρΝβ–ΈABCDΒΡ±Ώ≥ΛΈΣΘ® Θ©
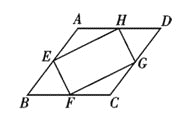
A. ![]() B. 2
B. 2 ![]() C. 2 D. 4
C. 2 D. 4
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
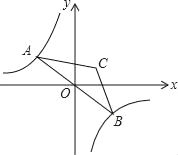
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΒψA «ΥΪ«ζœΏy=©¹![]() ‘ΎΒΎΕΰœσœόΖ÷÷ß…œΒΡ“ΜΗωΕ·ΒψΘ§Ν§Ϋ”AO≤Δ―”≥ΛΫΜΝμ“ΜΖ÷÷ß”ΎΒψBΘ§“‘ABΈΣΒΉΉςΒ»―ϋΓςABCΘ§«“ΓœACB=120ΓψΘ§ΒψC‘ΎΒΎ“ΜœσœόΘ§ΥφΉ≈ΒψAΒΡ‘ΥΕ·Θ§ΒψCΒΡΈΜ÷Ο“≤≤ΜΕœ±δΜ·Θ§ΒΪΒψC Φ÷’‘ΎΥΪ«ζœΏy=
‘ΎΒΎΕΰœσœόΖ÷÷ß…œΒΡ“ΜΗωΕ·ΒψΘ§Ν§Ϋ”AO≤Δ―”≥ΛΫΜΝμ“ΜΖ÷÷ß”ΎΒψBΘ§“‘ABΈΣΒΉΉςΒ»―ϋΓςABCΘ§«“ΓœACB=120ΓψΘ§ΒψC‘ΎΒΎ“ΜœσœόΘ§ΥφΉ≈ΒψAΒΡ‘ΥΕ·Θ§ΒψCΒΡΈΜ÷Ο“≤≤ΜΕœ±δΜ·Θ§ΒΪΒψC Φ÷’‘ΎΥΪ«ζœΏy=![]() …œ‘ΥΕ·Θ§‘ρkΒΡ÷ΒΈΣ_____Θ°
…œ‘ΥΕ·Θ§‘ρkΒΡ÷ΒΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
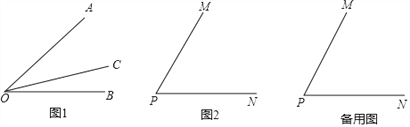
ΓΨΧβΡΩΓΩΓΨΧΫΥς–¬÷ΣΓΩΘΚ»γΆΦ1Θ§…δœΏOC‘ΎΓœAOBΒΡΡΎ≤ΩΘ§ΆΦ÷–Ι≤”–3ΗωΫ«ΘΚΓœAOBΘ§ΓœAOCΚΆΓœBOCΘ§»τΤδ÷–”–“ΜΗωΫ«ΒΡΕ» ΐ «Νμ“ΜΗωΫ«Ε» ΐΒΡΝΫ±ΕΘ§‘ρ≥Τ…δœΏOC «ΓœAOBΒΡΓΑ«…Ζ÷œΏΓ±Θ°
Θ®1Θ©“ΜΗωΫ«ΒΡΤΫΖ÷œΏΓΓ ΓΓ’βΗωΫ«ΒΡΓΑ«…Ζ÷œΏΓ±ΘΜΘ®ΧνΓΑ «Γ±ΜρΓΑ≤Μ «Γ±Θ©
Θ®2Θ©»γΆΦ2Θ§»τΓœMPN=ΠΝΘ§«“…δœΏPQ «ΓœMPNΒΡΓΑ«…Ζ÷œΏΓ±Θ§‘ρΓœMPQ=ΓΓ ΓΓΘΜΘ®”ΟΚ§ΠΝΒΡ¥ζ ΐ Ϋ±μ Ψ≥ωΥυ”–Ω…ΡήΒΡΫαΙϊΘ©
ΓΨ…ν»κ―–ΨΩΓΩΘΚ»γΆΦ2Θ§»τΓœMPN=60ΓψΘ§«“…δœΏPQ»ΤΒψP¥”PNΈΜ÷ΟΩΣ ΦΘ§“‘ΟΩΟκ10ΓψΒΡΥΌΕ»Ρφ ±’κ–ΐΉΣΘ§Β±PQ”κPN≥…180Γψ ±ΆΘ÷Ι–ΐΉΣΘ§–ΐΉΣΒΡ ±ΦδΈΣtΟκΘ°
Θ®3Θ©Β±tΈΣΚΈ÷Β ±Θ§…δœΏPM «ΓœQPNΒΡΓΑ«…Ζ÷œΏΓ±ΘΜ
Θ®4Θ©»τ…δœΏPMΆ§ ±»ΤΒψP“‘ΟΩΟκ5ΓψΒΡΥΌΕ»Ρφ ±’κ–ΐΉΣΘ§≤Δ”κPQΆ§ ±ΆΘ÷ΙΘ§«κ÷±Ϋ”–¥≥ωΒ±…δœΏPQ «ΓœMPNΒΡΓΑ«…Ζ÷œΏΓ± ±tΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣyΙΊ”ΎxΒΡΕΰ¥ΈΚ· ΐy=ax2©¹bx+2Θ®aΓΌ0Θ©Θ°
Θ®1Θ©Β±a=©¹2Θ§b=©¹4 ±Θ§«σΗΟΚ· ΐΆΦœσΒΡΕ‘≥Τ÷αΦΑΕΞΒψΉχ±ξΘ°
Θ®2Θ©‘ΎΘ®1Θ©ΒΡΧθΦΰœ¬Θ§QΘ®mΘ§tΘ©ΈΣΗΟΚ· ΐΆΦœσ…œΒΡ“ΜΒψΘ§»τQΙΊ”Ύ‘≠ΒψΒΡΕ‘≥ΤΒψP“≤¬δ‘ΎΗΟΚ· ΐΆΦœσ…œΘ§«σmΒΡ÷ΒΘ°
Θ®3Θ©Β±ΗΟΚ· ΐΆΦœσΨ≠ΙΐΒψΘ®1Θ§0Θ© ±Θ§»τAΘ®![]() Θ§y1Θ©Θ§BΘ®
Θ§y1Θ©Θ§BΘ®![]() Θ§y2Θ© «ΗΟΚ· ΐΆΦœσ…œΒΡΝΫΒψΘ§ ‘±»Ϋœy1”κy2ΒΡ¥σ–ΓΘ°
Θ§y2Θ© «ΗΟΚ· ΐΆΦœσ…œΒΡΝΫΒψΘ§ ‘±»Ϋœy1”κy2ΒΡ¥σ–ΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
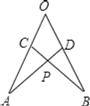
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓœAOBΒΡΝΫ±ΏΫΊ»ΓOA=OBΘ§OC=ODΘ§Ν§Ϋ”ADΘ§BCΫΜ”ΎΒψPΘ§‘ρœ¬Ν–Ϋα¬έ÷–ΔΌΓςAODΓ’ΓςBOCΘ§ΔΎΓςAPCΓ’ΓςBPDΘ§ΔέΒψP‘ΎΓœAOBΒΡΤΫΖ÷œΏ…œΘ°’ΐ»ΖΒΡ «__Θ°Θ®Χν–ρΚ≈Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΫβΦΉΓΔ““ΝΫΑύ”Δ”οΩΎ”οΥ°ΤΫΘ§ΟΩΑύΥφΜζ≥ι»ΓΝΥ10Οϊ―ß…ζΫχ––ΝΥΩΎ”ο≤β―ιΘ§≤β―ι≥…Φ®¬ζΖ÷ΈΣ10Ζ÷Θ§≤ΈΦ”≤β―ιΒΡ10Οϊ―ß…ζ≥…Φ®Θ®ΒΞΈΜΘΚΖ÷Θ©≥ΤΈΣ―υ±Ψ ΐΨίΘ§≥ι―υΒς≤ιΙΐ≥Χ»γœ¬ΘΚ
’Φ· ΐΨί
ΦΉΓΔ““ΝΫΑύΒΡ―υ±Ψ ΐΨίΖ÷±πΈΣΘΚ
ΦΉΑύΘΚ6 7 9 4 6 7 6 9 6 10
““ΑύΘΚ7 8 9 7 5 7 8 5 9 5
’ϊάμΚΆΟη ω ΐΨί
ΙφΕ®ΝΥΥΡΗω≤ψ¥ΈΘΚ9Ζ÷“‘…œΘ®Κ§9Ζ÷Θ©ΈΣΓΑ”≈–ψΓ±Θ§8-9Ζ÷Θ®Κ§8Ζ÷Θ©ΈΣΓΑΝΦΚΟΓ±Θ§6-8Ζ÷Θ®Κ§6Ζ÷Θ©ΈΣΓΑ“ΜΑψΓ±Θ§6Ζ÷“‘œ¬Θ®≤ΜΚ§6Ζ÷Θ©ΈΣΓΑ≤ΜΚœΗώΓ±ΓΘΑ¥“‘…œ≤ψ¥ΈΖ÷≤ΦΜφ÷Τ≥ω»γœ¬ΒΡ…»–ΈΆ≥ΦΤΆΦΓΘ


«κΦΤΥψΘΚΘ®1Θ©ΆΦ1÷–Θ§ΓΑ≤ΜΚœΗώΓ±≤ψ¥ΈΥυ’ΦΒΡΑΌΖ÷±»ΘΜ
Θ®2Θ©ΆΦ2÷–Θ§ΓΑ”≈–ψΓ±≤ψ¥ΈΕ‘”ΠΒΡ‘≤–ΡΫ«ΒΡΕ» ΐΓΘ
Ζ÷Έω ΐΨί
Ε‘”ΎΦΉΓΔ““ΝΫΑύΒΡ―υ±Ψ ΐΨίΘ§«κ÷±Ϋ”ΜΊ¥πΘΚ
Θ®1Θ©ΦΉΑύΒΡΤΫΨυ ΐ «7Θ§÷–ΈΜ ΐ «_____ΘΜ““ΑύΒΡΤΫΨυ ΐ «_____Θ§÷–ΈΜ ΐ «7ΘΜ
Θ®2Θ©¥”ΤΫΨυ ΐΚΆ÷–ΈΜ ΐΩ¥Θ§____Αύ’ϊΧε≥…Φ®ΗϋΚΟΓΘ
ΫβΨωΈ Χβ
»τΦΉΑύ50»ΥΘ§““Αύ40»ΥΘ§Ά®ΙΐΦΤΥψΘ§ΙάΦΤΦΉΓΔ““ΝΫΑύΓΑ≤ΜΚœΗώΓ±≤ψ¥ΈΒΡΙ≤”–Εύ…Ό»ΥΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com