
【题目】已知y关于x的二次函数y=ax2﹣bx+2(a≠0).
(1)当a=﹣2,b=﹣4时,求该函数图象的对称轴及顶点坐标.
(2)在(1)的条件下,Q(m,t)为该函数图象上的一点,若Q关于原点的对称点P也落在该函数图象上,求m的值.
(3)当该函数图象经过点(1,0)时,若A(![]() ,y1),B(
,y1),B(![]() ,y2)是该函数图象上的两点,试比较y1与y2的大小.
,y2)是该函数图象上的两点,试比较y1与y2的大小.
【答案】(1) 顶点坐标是(1,4),对称轴为直线x=1;(2) y1>y2.
【解析】分析:(1)将a、b的值代入函数解析式即可;
(2)根据(1)中的结论,即可求得m的值;
(3)根据题意和二次函数的性质,利用分类讨论的数学思想即可求得y1与y2的大小.
详解:(1)当a=-2,b=-4时,
y=-2x2+4x+2=-2(x-1)2+4,
∴该函数图象的顶点坐标是(1,4),对称轴为直线x=1;
(2)点Q(m,t)关于原点对称的点的坐标P是(-m,-t),
则![]() ,
,
解得,m=±1;
(3)∵函数的图象经过点(1,0),
∴0=a-b+2,
∴b=a+2,
∵y=ax2-bx+2,
∴函数的对称轴为直线x=![]() ,
,
当a>0时,![]() <
<![]() +
+![]() <
<![]() +
+![]() ,
,
∵![]() +
+![]() -
-![]() =
=![]() ,
,![]() +
+![]() -(
-(![]() +
+![]() )=
)=![]() ,A(
,A(![]() ,y1),B(
,y1),B(![]() +
+![]() ,y2)是该函数图象上的两点,
,y2)是该函数图象上的两点,
∴y2>y1,
当a<0时,![]() +
+![]() <
<![]() +
+![]() <
<![]() ,
,
∵![]() -(
-(![]() +
+![]() )=-
)=-![]() ,
,![]() +
+![]() -(
-(![]() +
+![]() )=-
)=-![]() ,A(
,A(![]() ,y1),B(
,y1),B(![]() +
+![]() ,y2)是该函数图象上的两点,
,y2)是该函数图象上的两点,
∴y1>y2.


科目:初中数学 来源: 题型:
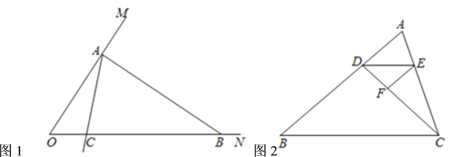
【题目】阅读下列材料并解答问题:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“3倍角三角形”例如:一个三角形三个内角的度数分别是![]() ,这个三角形就是一个“3倍角三角形”.反之,若一个三角形是“3倍角三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
,这个三角形就是一个“3倍角三角形”.反之,若一个三角形是“3倍角三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
(1)如图1,已知![]() ,在射线
,在射线![]() 上取一点
上取一点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .判断
.判断![]() 是否是“3倍角三角形”,为什么?
是否是“3倍角三角形”,为什么?
(2)在(1)的条件下,以![]() 为端点画射线
为端点画射线![]() ,交线段
,交线段![]() 于点
于点![]() (点
(点![]() 不与点
不与点![]() 、点
、点![]() 重合).若
重合).若![]() 是“3倍角三角形”,求
是“3倍角三角形”,求![]() 的度数.
的度数.
(3)如图2,点![]() 在
在![]() 的边上,连接
的边上,连接![]() ,作
,作![]() 的平分线交
的平分线交![]() 于点
于点![]() ,在
,在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,
,![]() .若
.若![]() 是“3倍角三角形”,求
是“3倍角三角形”,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期,我市持续出现雾霾天气,给广大市民的工作和生活造成了严重的影响.为此,“雾霾天气的主要成因”就成为了某校环保小组调查研究的课题,他们随机调查了部分市民,并对调查结果进行了整理,绘制了如图所示的不完整的统计图表.请根据图表中提供的信息解答下列问题:
级别 | 观点 | 频数(人数) |
A | 大气气压低,空气不流动 |
|
B | 地面灰尘大,空气湿度低 |
|
C | 汽车尾部排放 |
|
D | 工厂造成污染 |
|
E | 其他 |
|
调查结果扇形统计图
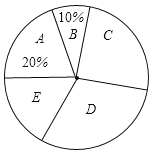
(1)填空:![]() ______,
______,![]() ______;
______;
(2)求出扇形统计图中E组所占的百分比以及扇形统计图中区域D所对应的扇形圆心角度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学学生步行到郊外旅行,七年级![]() 班学生组成前队,步行速度为4千米
班学生组成前队,步行速度为4千米![]() 小时,七
小时,七![]() 班的学生组成后队,速度为6千米
班的学生组成后队,速度为6千米![]() 小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米
小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米![]() 小时.
小时.
![]() 后队追上前队需要多长时间?
后队追上前队需要多长时间?
![]() 后队追上前队的时间内,联络员走的路程是多少?
后队追上前队的时间内,联络员走的路程是多少?
![]() 七年级
七年级![]() 班出发多少小时后两队相距2千米?
班出发多少小时后两队相距2千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形。
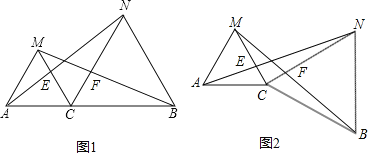
(1)△ACN≌△MCB吗?为什么?
(2)证明:CE=CF;
(3)若△CBN绕着点C旋转一定的角度(如图2),则上述2个结论还成立吗?
(4)若AN、MB相交于O,则∠AOB度数有没变化?若没有变化,则∠AOB= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出定义:我们用(a,b)来表示一对有理数a,b,若a,b满足a﹣b=ab+1,就称(a,b)是“泰兴数”如2﹣![]() +1,则(2,
+1,则(2,![]() )是“泰兴数”.
)是“泰兴数”.
(1)数对(﹣2,1),(5,![]() )中是“泰兴数”的是 .
)中是“泰兴数”的是 .
(2)若(m,n)是“泰兴数”,求6m﹣2(2m+mn)﹣2n的值;
(3)若(a,b)是“泰兴数”,则(﹣a,﹣b) “泰兴数”(填“是”或“不是”).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com