
【题目】阅读下列材料并解答问题:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“3倍角三角形”例如:一个三角形三个内角的度数分别是![]() ,这个三角形就是一个“3倍角三角形”.反之,若一个三角形是“3倍角三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
,这个三角形就是一个“3倍角三角形”.反之,若一个三角形是“3倍角三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
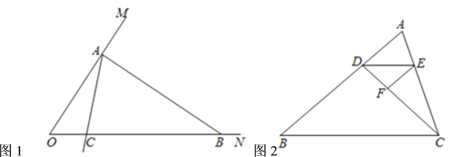
(1)如图1,已知![]() ,在射线
,在射线![]() 上取一点
上取一点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .判断
.判断![]() 是否是“3倍角三角形”,为什么?
是否是“3倍角三角形”,为什么?
(2)在(1)的条件下,以![]() 为端点画射线
为端点画射线![]() ,交线段
,交线段![]() 于点
于点![]() (点
(点![]() 不与点
不与点![]() 、点
、点![]() 重合).若
重合).若![]() 是“3倍角三角形”,求
是“3倍角三角形”,求![]() 的度数.
的度数.
(3)如图2,点![]() 在
在![]() 的边上,连接
的边上,连接![]() ,作
,作![]() 的平分线交
的平分线交![]() 于点
于点![]() ,在
,在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,
,![]() .若
.若![]() 是“3倍角三角形”,求
是“3倍角三角形”,求![]() 的度数.
的度数.
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于点Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 为线段
为线段![]() 上一点,点
上一点,点![]() 为
为![]() 的中点,且
的中点,且![]() ,
,![]() .
.
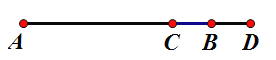
(1)图中共有______条线段,分别是______;
(2)求线段![]() 的长;
的长;
(3)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是( )
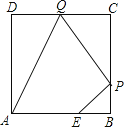
A. 3 B. 5 C. 4 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请补充完成以下解答过程,并在括号内填写该步骤的理由.已知:如图,![]() ,
,![]() ,OA平分
,OA平分![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.
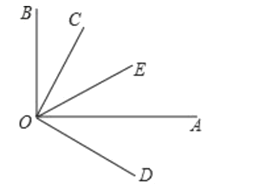
解:因为![]() ,
,
所以![]() ________
________![]() .
.
因为_________![]() ,
,
所以![]() .
.
所以![]() .(__________________)
.(__________________)
因为![]() ,
,
所以![]() .
.
因为OA平分![]() ,
,
所以__________![]() _______°
_______°
所以![]() _______°.
_______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
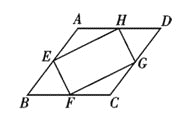
【题目】如图,在菱形ABCD中,点E,F,G,H分别是边AB,BC,CD和DA的中点,连接EF,FG,GH和HE,若EH=2EF=2,则菱形ABCD的边长为( )
A. ![]() B. 2
B. 2 ![]() C. 2 D. 4
C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
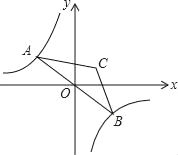
【题目】如图,点A是双曲线y=﹣![]() 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=![]() 上运动,则k的值为_____.
上运动,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y关于x的二次函数y=ax2﹣bx+2(a≠0).
(1)当a=﹣2,b=﹣4时,求该函数图象的对称轴及顶点坐标.
(2)在(1)的条件下,Q(m,t)为该函数图象上的一点,若Q关于原点的对称点P也落在该函数图象上,求m的值.
(3)当该函数图象经过点(1,0)时,若A(![]() ,y1),B(
,y1),B(![]() ,y2)是该函数图象上的两点,试比较y1与y2的大小.
,y2)是该函数图象上的两点,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴子A、B两点,与反比例函数y![]() 的图象交于C、D两点,DE⊥x轴于点E,已知点C的坐标是(6,-1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E,已知点C的坐标是(6,-1),DE=3.
(1)求反比例函数与一次函数的关系式;
(2)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com