
【题目】如图,点![]() 为线段
为线段![]() 上一点,点
上一点,点![]() 为
为![]() 的中点,且
的中点,且![]() ,
,![]() .
.
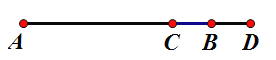
(1)图中共有______条线段,分别是______;
(2)求线段![]() 的长;
的长;
(3)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)6,分别为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据线段的定义即可得结论;
(2)根据线段的中点定义及线段的和即可求解;
(3)分点E在点A的左右两侧两种情况进行计算即可.
(1)图中共有6条线段,分别是:AC、AB、AD、CB、CD、BD;
(2)∵点B是CD的中点,BD=2,
∴CD=2BD=4,
∴AD=AC+CD=10,
答:AD的长为10cm;
(3)当点E在点A左侧时,如图:
![]()
∵点B是线段CD的中点,
∴BC=BD=2,
∴AB=AC+BC=8,
∴BE=AE+AB=3+=11,
当点E在点A右侧时,如图:
![]()
BE=AB-AE=8-3=5.
答:BE的长为11cm或5cm.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,网格图由边长为1的小正方形所构成,Rt△ABC的顶点分别是A(-1,3),B(-3,-1),C(-3,3).

(1)请在图1中作出△ABC关于点(-1,0)成中心对称△![]() ,并分别写出A,C对应点的坐标
,并分别写出A,C对应点的坐标![]() ;
;![]()
(2)设线段AB所在直线的函数表达式为![]() ,试写出不等式
,试写出不等式![]() 的解集是 ;
的解集是 ;
(3)点M和点N 分别是直线AB和y轴上的动点,若以![]() ,
,![]() ,M,N为顶点的四边形是平行四边形,求满足条件的M点坐标.
,M,N为顶点的四边形是平行四边形,求满足条件的M点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
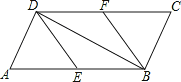
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.邮箱中剩余油量Q(L)与行驶时间t(h)之间的函数关系如图所示.
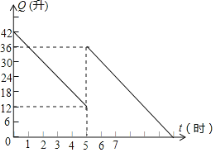
(1)汽车行驶 h后加油,加油量为 L;
(2)求加油前油箱剩余油量Q与行驶时间t之间的函数关系式;
(3)如果加油站离目的地还有200km,车速为40km/h,请直接写出汽车到达目的地时,油箱中还有多少汽油?
查看答案和解析>>
科目:初中数学 来源: 题型:
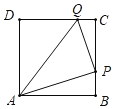
【题目】已知,如图,正方形![]() 的边长为4厘米,点
的边长为4厘米,点![]() 从点
从点![]() 出发,经
出发,经![]() 沿正方形的边以2厘米/秒的速度运动;同时,点
沿正方形的边以2厘米/秒的速度运动;同时,点![]() 从点
从点![]() 出发以1厘米/秒的速度沿
出发以1厘米/秒的速度沿![]() 向点
向点![]() 运动,设运动时间为t秒,
运动,设运动时间为t秒,![]() 的面积为
的面积为![]() 平方厘米.
平方厘米.
(1)当![]() 时,
时,![]() 的面积为__________平方厘米;
的面积为__________平方厘米;
(2)求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(3)当点![]() 在线段
在线段![]() 上运动,且
上运动,且![]() 为等腰三角形时,求此时
为等腰三角形时,求此时![]() 的值;
的值;
(4)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 的对角线相交于点
的对角线相交于点![]() ,
,![]() ,
,![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)若将题设中“矩形![]() ”这一条件改为“菱形
”这一条件改为“菱形![]() ”,其余条件不变,则四边形
”,其余条件不变,则四边形![]() 是__________形.
是__________形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解答问题:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“3倍角三角形”例如:一个三角形三个内角的度数分别是![]() ,这个三角形就是一个“3倍角三角形”.反之,若一个三角形是“3倍角三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
,这个三角形就是一个“3倍角三角形”.反之,若一个三角形是“3倍角三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
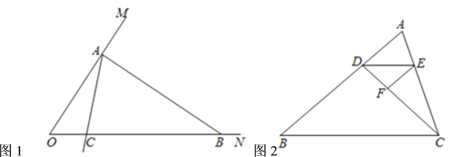
(1)如图1,已知![]() ,在射线
,在射线![]() 上取一点
上取一点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .判断
.判断![]() 是否是“3倍角三角形”,为什么?
是否是“3倍角三角形”,为什么?
(2)在(1)的条件下,以![]() 为端点画射线
为端点画射线![]() ,交线段
,交线段![]() 于点
于点![]() (点
(点![]() 不与点
不与点![]() 、点
、点![]() 重合).若
重合).若![]() 是“3倍角三角形”,求
是“3倍角三角形”,求![]() 的度数.
的度数.
(3)如图2,点![]() 在
在![]() 的边上,连接
的边上,连接![]() ,作
,作![]() 的平分线交
的平分线交![]() 于点
于点![]() ,在
,在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,
,![]() .若
.若![]() 是“3倍角三角形”,求
是“3倍角三角形”,求![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com